Пример. Линейная регрессия
Используйте функции polyfitc, line, slope и intercept, чтобы найти линию аппроксимации по методу наименьших квадратов в наборе данных x-y. Используйте функцию stderr для расчета ошибки в подгоночных параметрах. Рассчитайте доверительные пределы вокруг линии наилучшего приближения и сформируйте доверительные интервалы.
Линия наилучшего приближения
Создайте линейную функцию, чтобы оценить, как много времени потребуется, чтобы проехать то или иное расстояние.
1. Определите набор расстояний в милях и время в минутах, необходимое для того, чтобы проехать эти расстояния.
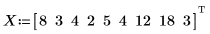
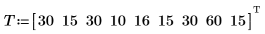
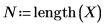
2. Определите одномерное уравнение линейной регрессии.
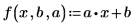
3. Вызовите функцию polyfitc, чтобы рассчитать коэффициенты регрессии a и b.
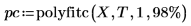
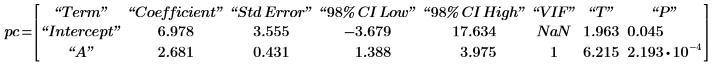
Эти коэффициенты таковы, что разница между значениями в T и значениями, рассчитанными уравнением регрессии f, минимальна для каждого значения.x. Это можно проверить, используя блок решения и функцию minimize для минимизации суммы квадратов:

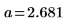
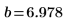
4. Определите линию наилучшего приближения, чтобы минимизировать сумму квадратов расстояний от каждой точки до линии.
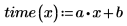
Необходимо использовать параметризованное уравнение из линейного или любого другого типа регрессии только для значений, близких к исходным наблюдаемым данным. Линия наилучшего приближения для приведенных выше данных позволяет предсказать, что на преодоление расстояния в 0 миль потребуется следующее время:
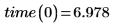
Это не имеет смысла, если измеренное время является строго временем пути при постоянной скорости. Такой результат может иногда представлять определенный физический феномен. В данном случае время, требуемое на покрытие нулевого расстояния, может быть интерпретировано как среднее время ожидания на светофорах.
5. Распечатайте точки данных и линию наилучшего приближения.
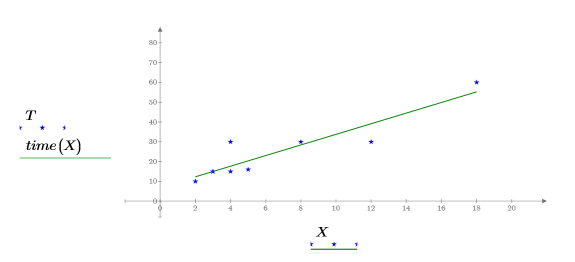
Альтернативные методы расчета наклона и отрезка
Существует несколько методов расчета наклона и отрезка, отсекаемого на оси, для линии наилучшего приближения. Например, функция line сочетает функции slope и intercept. Другие методы включают матричные вычисления или статистические зависимости.
1. Вызовите функции intercept и slope.
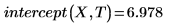
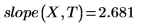
2. Вызовите функцию line.
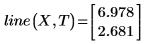
3. Используйте матричные вычисления, применяя функцию augment.
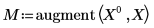
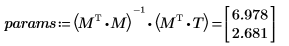
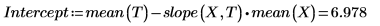
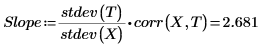
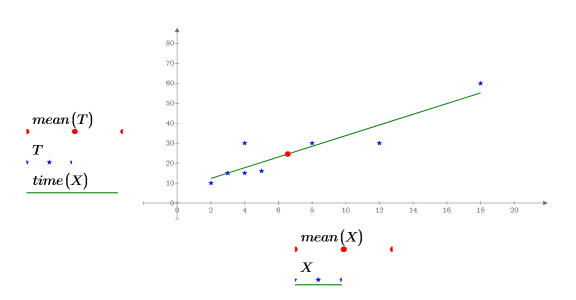
5. Используйте график, чтобы показать, что линия наименьших квадратов всегда проходит через точку (mean(X), mean(T)):
Среднеквадратические ошибки
Рассчитайте среднеквадратическую ошибку оценки (ее также называют стандартной ошибкой), чтобы измерить, насколько точно линейное приближение, приведенное выше. Также рассчитайте ошибку наклона и отрезка, отсекаемого на оси.
1. Определите степени свободы (количество точек данных минус количество подобранных параметров).
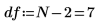
2. Вызовите функцию stderr, чтобы рассчитать среднеквадратическую ошибку оценки для линии наилучшего приближения, определенной выше.
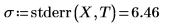
Это квадратный корень среднего квадрата ошибки, среднеквадратическая ошибка или σ2:
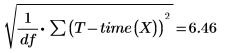
3. Сравните расчетную среднеквадратическую ошибку со среднеквадратической ошибкой, возвращенной функцией polyfitstat.
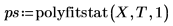
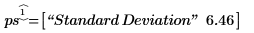
4. Рассчитайте среднеквадратические ошибки наклона и точки пересечения.
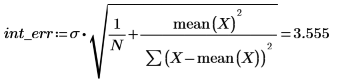
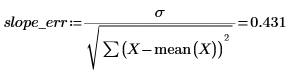
5. Повторите вышеупомянутый расчет, используя матричные вычисления.
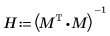
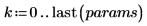
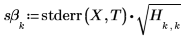
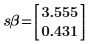
6. Используйте функцию augment, чтобы показать, что среднеквадратические ошибки для каждого коэффициента регрессии записаны в матрице, возвращенной функцией polyfitc.
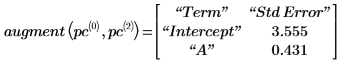
Доверительные интервалы для каждого коэффициента
Используйте приведенные выше виды оценки вместе с процентильными точками из распределения Стьюдента, чтобы сформировать доверительный интервал для оценок наклона и отсекаемого на оси отрезка.
1. Определите уровень значимости для доверительного интервала 98% и используйте функцию qt для расчета t-фактора.
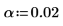
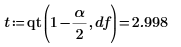
2. Рассчитайте доверительные пределы для наклона.
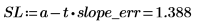
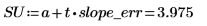
Существует вероятность 98%, что фактическим значением наклона является значение между SL и SU.
3. Рассчитайте доверительные пределы для отрезка, отсекаемого на оси.
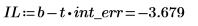
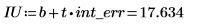
Широкий диапазон для этого значения отражает высокий уровень разброса данных.
4. Вызовите функцию confidence, чтобы повторить шаги 1 и 3.
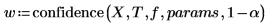
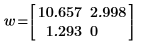
Функция confidence возвращает ширину доверительного интервала в первом столбце и t-коэффициент во втором столбце. При делении ширины на t-коэффициент мы получаем среднеквадратические ошибки для обоих параметров:
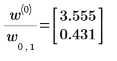
5. Чтобы найти доверительные пределы, можно добавить или вычесть ширину из соответствующего параметра:
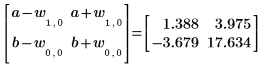
6. Используйте функцию augment, чтобы показать, что среднеквадратические ошибки для каждого коэффициента регрессии записаны в матрице, возвращенной функцией polyfitc.

Доверительные интервалы для регрессии
1. Используйте функции length и mean, чтобы вычислить доверительный интервал для регрессии непосредственно.
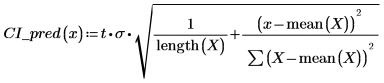
2. Используйте предыдущую функцию, чтобы вычислить доверительный интервал для любого прогнозируемого значения x:
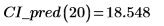
3. Используйте матричные вычисления:
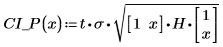
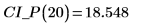
4. Распечатайте данные, линию наилучшего приближения и доверительный интервал для всей области регрессии.
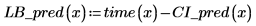
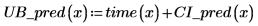
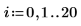
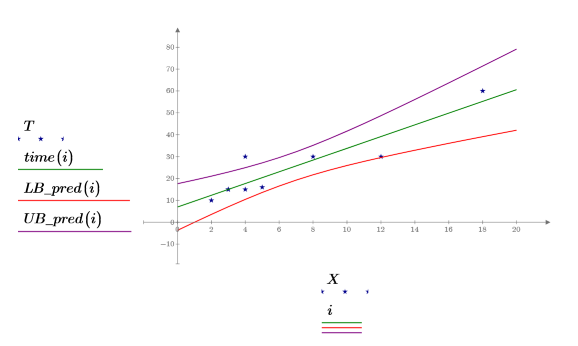
Доверительная область для прогнозируемых значений сужается возле центра измеренных значений. Это происходит потому, что формулы, использованные для расчета линейной регрессии, основаны на среднем значении, поэтому чем ближе прогнозируемое значение к среднему по данным, тем оно точнее.
5. Рассчитайте доверительные пределы для измеренных значений. Эти пределы немного отличаются от пределов для прогнозируемых значений.
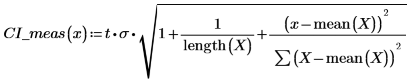
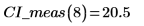
6. Используйте матричные вычисления:
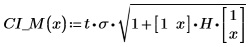
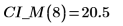
7. Постройте график доверительных пределов как кривую погрешности.
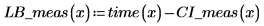
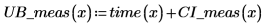
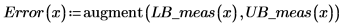
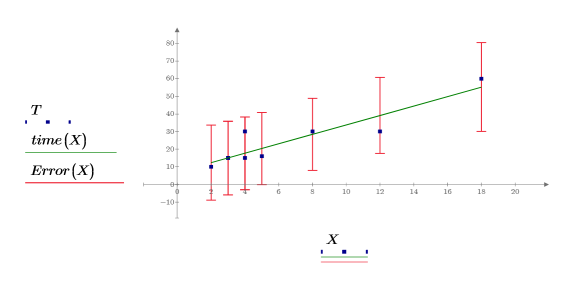
Можно использовать графики как средство обнаружения отклонения, где измеренные значения, попадающие за пределы доверительных интервалов, указывают на отклонение. |