Дисперсия и среднеквадратическое отклонение

Функции > Статистика > Описательная статистика > Дисперсия и среднеквадратическое отклонение

Дисперсия и среднеквадратическое отклонение

Следующие две функции возвращают дисперсию и среднеквадратическое отклонение совокупности с дисперсией, заданной следующим образом:

<region id="ID0EOAMAB" top="57.600000000000009" left="57.600000000000009" height="50.000000000000007" width="256.06" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="4">
    <apply xmlns="http://schemas.mathsoft.com/math50">
      <mult />
      <parens>
        <apply>
          <div />
          <real>1</real>
          <apply>
            <mult />
            <id xml:space="preserve">m</id>
            <id xml:space="preserve">n</id>
          </apply>
        </apply>
      </parens>
      <apply>
        <summation />
        <lambda>
          <boundVars>
            <id xml:space="preserve">i</id>
          </boundVars>
          <apply>
            <summation />
            <lambda>
              <boundVars>
                <id xml:space="preserve">j</id>
              </boundVars>
              <apply>
                <pow />
                <parens>
                  <apply>
                    <minus />
                    <apply>
                      <indexer />
                      <id xml:space="preserve">M</id>
                      <sequence>
                        <id xml:space="preserve">i</id>
                        <id xml:space="preserve">j</id>
                      </sequence>
                    </apply>
                    <apply>
                      <id xml:space="preserve">mean</id>
                      <id xml:space="preserve">M</id>
                    </apply>
                  </apply>
                </parens>
                <real>2</real>
              </apply>
            </lambda>
            <lowerBound>
              <real>0</real>
            </lowerBound>
            <upperBound>
              <apply>
                <minus />
                <id xml:space="preserve">n</id>
                <real>1</real>
              </apply>
            </upperBound>
          </apply>
        </lambda>
        <lowerBound>
          <real>9</real>
        </lowerBound>
        <upperBound>
          <apply>
            <minus />
            <id xml:space="preserve">m</id>
            <real>1</real>
          </apply>
        </upperBound>
      </apply>
    </apply>
  </math>
</region>

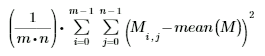
• var(A, B, C, ...) — возвращает дисперсию совокупности элементов A, B, C, ...;

• stdev(A, B, C, ...) — возвращает квадратный корень из дисперсии совокупности элементов A, B, C, ....

Следующие две функции возвращают дисперсию и среднеквадратическое отклонение выборки с дисперсией, заданной следующим образом:

<region id="ID0EYDMAB" top="134.40000000000003" left="57.600000000000009" height="50.000000000000007" width="278.79" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="6">
    <apply xmlns="http://schemas.mathsoft.com/math50">
      <mult />
      <parens>
        <apply>
          <div />
          <real>1</real>
          <apply>
            <minus />
            <apply>
              <mult />
              <id xml:space="preserve">m</id>
              <id xml:space="preserve">n</id>
            </apply>
            <real>1</real>
          </apply>
        </apply>
      </parens>
      <apply>
        <summation />
        <lambda>
          <boundVars>
            <id xml:space="preserve">i</id>
          </boundVars>
          <apply>
            <summation />
            <lambda>
              <boundVars>
                <id xml:space="preserve">j</id>
              </boundVars>
              <apply>
                <pow />
                <parens>
                  <apply>
                    <minus />
                    <apply>
                      <indexer />
                      <id xml:space="preserve">M</id>
                      <sequence>
                        <id xml:space="preserve">i</id>
                        <id xml:space="preserve">j</id>
                      </sequence>
                    </apply>
                    <apply>
                      <id xml:space="preserve">mean</id>
                      <id xml:space="preserve">M</id>
                    </apply>
                  </apply>
                </parens>
                <real>2</real>
              </apply>
            </lambda>
            <lowerBound>
              <real>0</real>
            </lowerBound>
            <upperBound>
              <apply>
                <minus />
                <id xml:space="preserve">n</id>
                <real>1</real>
              </apply>
            </upperBound>
          </apply>
        </lambda>
        <lowerBound>
          <real>0</real>
        </lowerBound>
        <upperBound>
          <apply>
            <minus />
            <id xml:space="preserve">m</id>
            <real>1</real>
          </apply>
        </upperBound>
      </apply>
    </apply>
  </math>
</region>

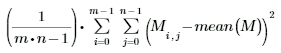
• Var(A, B, C, ...) — возвращает дисперсию выборки элементов A, B, C, ... ;

• Stdev(A, B, C, ...) — возвращает квадратный корень из дисперсии выборки элементов A, B, C, ....

Дисперсия и среднеквадратическое отклонения совокупности делятся на t (общее число значений), в отличие от дисперсии и среднеквадратического отклонения выборки, которые делятся на t – 1. Деление дисперсий, возведенных в квадрат, на размер выборки минус один в отличие от деления на полный размер выборки предоставляет более лучшую оценку для дисперсии истинной совокупности. Функции совокупности и выборки отличаются регистром первой буквы, поэтому будьте осторожны при вводе имени функции.

Хотя дисперсия предназначена для всеобщего измерения размаха распределения, она значительно подвержена влиянию "поведения хвоста".

Аргументы

• A, B, C, ... — скаляры или массивы размерности m x n.

• M — массив, созданный из аргументов функции A, B, C, ....

Похожие темы

Сведения об описательных статистических функциях

Пример. Дисперсия и среднеквадратическое отклонение

Пример. Линейная регрессия

Было ли это полезно?