Статистика многомерной полиномиальной регрессии
• Функция polyfitstat(X, Y, n/"terms"/M, [conf]) возвращает статистические данные о модели полиномиальной регрессии, аппроксимирующей результаты, записанные в матрице Y, к данным, содержащимся в матрице X. Уравнение полиномиальной регрессии можно определить, задав степень полинома n, или при помощи его членов, как указано в строке “terms” или в матрице M. Используйте матрицу M, если в аппроксимацию полиномом не требуется включать пересечение. Используйте дополнительный аргумент conf, чтобы указать доверительный интервал, отличающийся от заданного по умолчанию значения 95 %.
Второй столбец матрицы, возвращаемой функцией polyfitstat, содержит следующие элементы.
|
Строка
|
Описание
|
|---|---|
|
1
|
Среднеквадратическое отклонение для Y
|
|
2, 3, 4
|
R2, корректированный R2 и предсказанный R2
|
|
5
|
PRESS — сумма квадратов ошибок по предсказанию (применяется для масштабирования остатков)
|
|
6
|
Статистика Дарбина-Уотсона для автокорреляции
|
|
7
|
Матрица коэффициентов регрессии, возвращенных функцией polyfitc
|
|
8
|
Матрица ANOVA для модели регрессии с такими же столбцами, как в таблице результатов, возвращаемой функцией anova и следующими строками.
• Регрессия — промежуточная сумма, которая затем разбивается по всем элементам (исключая пересечение).
• Остаток (погрешность) — промежуточная сумма, которая затем разбивается на погрешность аппроксимации и чистую погрешность эксперимента.
• Общая сумма для модели регрессии.
|
|
9
|
Матрица диагностики со следующими столбцами.
1. Нумерация каждого выполнения или точки данных.
2. Наблюдаемый результат по каждому выполнению или точке данных.
3. Предсказанный в ходе исследования результат с помощью модели регрессии.
4. Остаток — разность между наблюдаемым и предсказанным результатом.
5. Сила — мера расстояния от наблюдаемого результата до точки, находящейся в центре всех наблюдаемых результатов.
6. Остаток по Стьюденту — остаток, деленный на дисперсию, рассчитанную по наблюдаемым результатам.
7. R-Стьюдент — остаток, деленный на дисперсию, рассчитанную по набору данных, из которого удалены наблюдаемые результаты.
8. Расстояние Кука — мера влияния наблюдаемых результатов на все другие точки данных.
9. DFFITS — разность между результатом, предсказанным с помощью модели регрессии, построенной по набору данных, в который включены наблюдаемые результаты, и результатом, предсказанным с помощью другой модели, из которой наблюдаемые результаты исключены.
|
Аргументы
• X — матрица плана или матрица, в которой каждый столбец представляет независимую переменную. Каждый столбец X должен иметь совместимые единицы измерения.
• Y — вектор или матрица с результатами измерений или моделирования, где каждая строка содержит результаты отдельного выполнения или точку данных, определенную в X. Если строки содержат неодинаковое число реплик, необходимо заполнить пустые элементы Y значениями NaN. Элементы Y должны иметь совместимые единицы измерения.
• n — целое число, определяющее степень полинома. Оно должно быть меньше общего числа точек данных: 1 ≤ n ≤ length(Y) − 1. В противном случае задача окажется под ограничением, которое не позволит получить уникальное решение.
• “terms” — строка, содержащая элементы или факторы и взаимодействия, которые требуется включить в полиномиальную регрессию. Строка "A B AB AA BB" означает, что полином содержит следующие члены.
c0 + c1 ∙ A + c2 ∙ B + c3 ∙ A ∙ B + c4 ∙ A2 + c5 ∙ B2
В качестве разделителя можно использовать пробел, запятую, двоеточие или точку с запятой.
• M — матрица, задающая полином, с начальными значениями коэффициентов в первом столбце и показателями степени независимых переменных для каждого члена в остальных столбцах. Для описанного выше полинома определите матрицу M следующим образом.
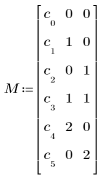
• conf (необязательный) — требуемый доверительный предел, доля, выраженная числом в интервале от 0 до 1 включительно. По умолчанию conf = 0.95 для доверительного интервала составляет 95 %.