Решатели ОДУ
• Каждая из приведенных ниже функций возвращает матрицу решения (intvls+1)×(n+1), где n представляет количество неизвестных. Первый столбец матрицы содержит значения x, в которых вычисляются решения. Это (intvls + 1) значений, равномерно распределенных между x1 и x2. Остальные столбцы содержат значения решений y0, y1, ..., yn-1, соответствующие значениям x в первом столбце.
• Для решателей rkfixed, RkAdapt, Bulstoer, Stiffb и Stiffr можно указать скалярную величину допуска решения, определив переменную TOL перед тем, как вызвать решатель. Например, можно задать для всех переменных допуск, равный 10-6:
TOL:= 10-6
TOL не влияет на допуски для решателей Adams, BDF или Radau. Для этих решателей необходимо использовать необязательный аргумент tol, чтобы указать допуски.
• Можно использовать блоки решений ОДУ, чтобы упростить запись уравнений и начальных условий.
Решатели для нежестких систем
• Adams(init, x1, x2, intvls, D, [tol]): использует методы Адамса.
• rkfixed(init, x1, x2, intvls, D): использует метод Рунге — Кутты четвертого порядка с фиксированным шагом.
• Rkadapt(init, x1, x2, intvls, D): использует метод Рунге — Кутты четвертого порядка с адаптационным размером шага.
• Bulstoer(init, x1, x2, intvls, D): использует метод Булирша — Штера, немного более точный, чем метод Рунге — Кутты, но требующий гладко меняющейся системы.
Решатели для жестких систем
Эти функции используются для решения задач с жесткими или алгебраическими ОДУ.
• BDF(init, x1, x2, intvls, D, [J], [tol]): использует методы формулы дифференцирования назад. Можно использовать один из необязательных аргументов J или tol и не использовать другой.
• Radau(init, x1, x2, intvls, D, [J], [M], [tol]): использует метод Радау5. Можно использовать любую комбинацию необязательных аргументов J, M и tol, опуская опции, необходимости в которых нет.
• Stiffb(init, x1, x2, intvls, D, AJ): использует метод Булирша — Штера.
• Stiffr(init, x1, x2, intvls, D, AJ): использует метод Розенброка.
Гибридный решатель
• AdamsBDF(init, x1, x2, intvls, D, [J], [tol]): определяет, является ли система жесткой или нежесткой, и вызывает Adams или BDF соответственно. Можно использовать один из необязательных аргументов J или tol и не использовать другой.
Аргументы
• init является либо вектором n начальных значений, где n представляет количество неизвестных, либо одним скалярным начальным значением в случае единственного уравнения ОДУ.
• x1 и x2 являются вещественными скалярными конечными точками интервала, для которого вычисляется решение уравнений ОДУ. Начальные значения в init являются значениями функций ОДУ, вычисленными в точке x1.
• intvls — целое число, количество интервалов дискретизации, используемое при интерполяции функции решения. Количество точек решения равняется количеству интервалов + 1.
• D является векторной функцией формы D(x,y), указывающей правую сторону системы.
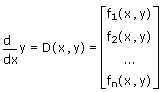
• tol (необязательно) является вещественным значением или вектором вещественных значений, указывающим допуски для каждой независимой переменной в системе. Допуск представляет собой требуемую точность переменной решения.
◦ Необходимо задать значение tol меньше или равным 10-5. В зависимости от масштаба проблемы и от используемого относительного размера шага может возникнуть необходимость уменьшить значение TOL для получения подходящих решений. Чем меньше значение tol, тем больше шагов выполняет алгоритм решателя для достижения требуемой точности.
◦ В случае решения системы уравнений задание значения tol как скалярной величины указывает один допуск для всех переменных в системе. Задание значения tol как вектора с длиной, равной числу переменных в системе, указывает индивидуальный допуск для каждой из переменных.
• J (необязательно) является функцией вида J(x, y), которая возвращает якобиан частных производных функций в D по y0, y1, ... yn−1.
• M (необязательно) является вещественной матрицей, представляющей любое соединение переменных в форме M · dy/dt = f(t, y).
• AJ является функцией формы AJ(x, y), возвращающей пополненный якобиан функций правой стороны системы, в первом столбце которого содержатся частные производные по x. Остальные столбцы являются столбцами якобиана J, содержащими частные производные по y0, y1, ... yn−1.
Функции D, J и AJ поступают в решатель без аргументов, а функции yn(x) указаны в D, J и AJ без аргумента.
Второй аргумент для D, J и AJ как вектор должен иметь подстрочный индекс, даже если есть только одна запись.
Дополнительная информация
• При решении дифференциального уравнения функции Radau и Rkadapt внутренне используют неравномерные шаги и добавляют дополнительные шаги в областях большего изменения решения, но возвращают решение в равномерно распределенных точках, количество которых указано в аргументе intvls.
• Преимущество использования функции Radau состоит в том, что не требуется вводить якобиан, хотя если значение J доступно, использование этой переменной повышает точность.