Решение ОДУ
Для поиска функции, удовлетворяющей обыкновенному дифференциальному уравнению (ОДУ) в заданном диапазоне значений, можно использовать блоки решения и функцию odesolve.
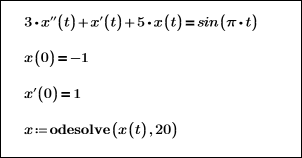
Здесь выходная функция рассчитана в диапазоне 0 ≤ x ≤ 20:
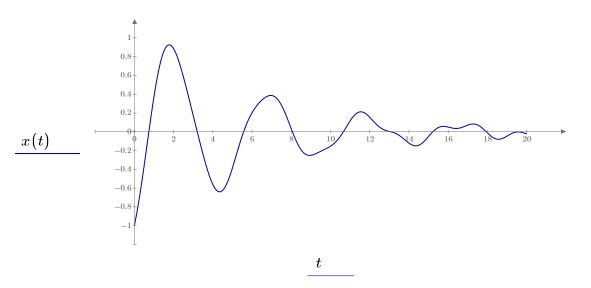
При использовании ОДУ в блоках решения необходимо учитывать следующие ограничения.
• Операторы. Для решения ОДУ в блоках решения используйте оператор "равно". Не используйте операторы сравнения или неравенства. Для определения производных используйте оператор производной или оператор штрих, например d/dx и d2/dx2 или y'(x) и y''(x).
• Начальные и граничные условия. Для одного ОДУ n-го порядка должно быть задано n независимых ограничений в форме равенства:
◦ Задача с начальными условиями. Требуются значения функции y(x) и первых n − 1 ее производных в одной начальной точке a.
◦ Граничная задача. n ограничений должны задавать определенные значения функции y(x) и ее производных в начальной точке a или в конечной точке b. Ограничения должны удовлетворять требованиям, предъявляемым к аргументам функции sbval. Функция odesolve вызывает функцию sbval в тех случаях, когда заданы граничные условия.
В любом случае конечные точки, используемые в граничных условиях, должны соответствовать конечным точкам, указанным в команде odesolve. PTC Mathcad проверяет правильность типа и количества условий и возвращает ошибку при обнаружении несоответствия.
• Алгебраические ограничения. Можно задать алгебраические ограничения, например y(b) + z(b) = w(b). В этом случае блок решения содержит одну дополнительную неизвестную функцию w, которую необходимо указывать в качестве одной из выходных функций odesolve.
• Результат. Результат вычислений функции odesolve необходимо назначить либо имени функции, либо вектору имен функций, без аргументов.
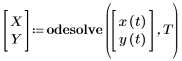
Неявным аргументом для этих функций является переменная интегрирования:
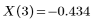
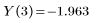
Методы решения
• В зависимости от масштаба задачи и используемого относительного размера шага может потребоваться уменьшить значение TOL, чтобы получить приемлемые решения. Попробуйте сделать это, когда функция PTC Mathcad odesolve сообщает о слишком большом числе шагов интегрирования.
• Функции, для которых находится решение, не должны содержать сингулярности в интервале интегрирования. В противном случае могут быть получены ненадежные результаты.
• При решении задач с периодическими функциями на интервалах, включающих много циклов, могут возникнуть псевдонимы. Чтобы получить требуемые частоты в результатах решения, увеличьте количество точек интерполяции.
• При решении обыкновенного дифференциального уравнения (ОДУ), в котором члены, содержащие производные высшего порядка, не являются линейными, или при решении системы ОДУ с помощью программного цикла используйте функцию rkfixed или какой-либо другой решатель ОДУ, вызываемый из командной строки. Результат вычислений параметризованного блока решения в программном цикле можно назначить также с помощью локальных функций.