Решатель ОДУ, использующий пространство состояний
• Функция statespace(init, t1, t2, intvls, A, [B, u]) возвращает решение системы обыкновенных линейных дифференциальных уравнений первого порядка следующей формы:
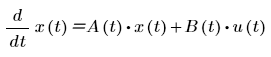
где
◦ x(t)
вектор неизвестных состояний.
◦ A(t)
матрица связи или матрица состояний между функциями и вектором x(t).
◦ B(t)
входная матрица, описывающая связи между элементами во входном векторе u(t).
◦ u(t) — входной вектор.
Функция возвращает матрицу решения (intvls+1)×(n+1), где n - число неизвестных состояний. Первый столбец матрицы содержит значения t, в которых вычисляются решения. Это (intvls+1) значений, равномерно распределенных между t1 и t2. Остальные столбцы содержат значения решений x0, x1, ..., xn-1, соответствующие значениям t из первого столбца.
Аргументы
• init — вектор-столбец начальных условий, длина которого равна числу неизвестных состояний.
• t1 — действительное число, задающее начальную точку интервала интегрирования.
• t2 — действительное число, задающее конечную точку интервала интегрирования.
• intvls — целое число, количество интервалов дискретизации, используемое при интерполяции функции решения. Количество точек решения равняется количеству интервалов + 1.
• A является матрицей-функцией размером n × n вида A(t), где n — число неизвестных состояний. Элементами A(t) являются функции независимой переменной t.
• B (необязательный) - матрица n × k или вектор-функция вида B(t), элементами которой являются функции t.
• u (необязательный) - вектор k × 1 или действительная скалярная функция вида u(t), элементами которой являются функции t.
Аргумент u является обязательным, если задан аргумент B.
• x (необязательный) - вектор k × 1 или действительная скалярная функция вида x(t), элементами которой являются функции t.
Аргумент x является обязательным, если задан аргумент A.
Дополнительная информация
Такая запись, где x(t) представляет вектор неизвестных для независимой переменной t, отличается от записи, используемой в Справке по другим решателям ОДУ, где буква x обозначает независимую переменную, а y(x) представляет вектор неизвестных.