Определение начальных условий для ОДУ
При решении граничных задач, когда известны не все начальные условия, используются следующие функции.
• bvalfit(v1, v2, x1, x2, xf, D, load1, load2, scoreb)
• sbval(v1, x1, x2, D, load1, scorei)
Возвращает вектор, содержащий те начальные значения, которые не были указаны в x1, для ОДУ или системы ОДУ, заданных в D. Эти начальные значения можно будет затем использовать в одном из решателей ОДУ. Если известны некоторые значения решения и его первые n − 1 производных в промежуточном значении, используйте функцию bvalfit, особенно полезную, когда производная имеет нарушение непрерывности в интервале интегрирования. Если известны некоторые значения в начальных и конечных точках, используйте функцию sbval. Граничная задача преобразуется в начальную при съемке из начальных точек и сопоставлении траекторий решений и их производных в промежуточной точке.
Аргументы
• v1, v2 — векторы из вещественных значений — начальных приближений, не указанных в x1.
• x1, x2 — вещественные значения — конечные точки интервала, на котором ищется решение дифференциальных уравнений.
• xf — вещественное значение — промежуточная точка между x1 и x2, в которой траектории решений должны сходиться.
• D(x, y) — функция, принимающая значения в виде n-элементных векторов, от независимой переменной x и вектора функций y, содержащего уравнения первых производных всех неизвестных функций в системе ОДУ.
Чтобы создать этот вектор, составьте уравнения так, чтобы члены, содержащие первые производные, были в левой части и без множителей и чтобы в уравнениях не было производных более высокого порядка. Например, ОДУ функции y(x) со второй производной необходимо записать в виде системы уравнений с y0(x) и y1(x), где первой производной y0 является y1. Следующее ОДУ с одной функцией переписано для решателя с помощью векторных индексов:
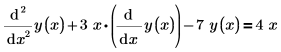
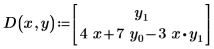 | с предполагаемой левой частью. | 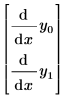 |
• load1(x1, v1), load2(x2, v2) — действительные функции, принимающие значения в виде векторов, элементы которых соответствуют значениям yn в x1 и x2 соответственно. Некоторые из этих значений являются известными начальными условиями. Неизвестные значения приравниваются к соответствующим начальным значениям из v1 и v2 соответственно.
• scoreb(xf, y) — действительная функция, принимающая значения в виде векторов, используемая для указания способа схождения решений в xf. Обычно требуется определить scoreb(xf, y):= y, чтобы решения всех неизвестных функций сошлись в xf.
• scorei(x2, y) — действительная функция, принимающая значения в виде векторов, с таким же числом элементов, как и v. Каждый элемент является разностью между начальным условием в x2, как было изначально задано, и соответствующей оценкой решателя. Вектор score служит мерой того, насколько точно предлагаемое решение соответствует начальным условиям в x2. Значение 0 у любого элемента указывает на точное соответствие.