Física
Para un flujo multicomponente, se resuelven las ecuaciones de transporte escalar para la velocidad de mezcla, la presión, la temperatura, la turbulencia y otras cantidades físicas. Cuando existen varios componentes, se deben resolver ecuaciones adicionales para determinar cómo se transportan los componentes dentro de la mezcla de fluidos.
Descripción de las distintas especies (componentes)
Existen varias variables diferentes, pero relacionadas, para cuantificar el contenido de un componente  del flujo de componentes
del flujo de componentes 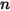 :
:
 del flujo de componentes
del flujo de componentes 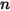 :
: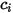 | concentración molar del componente  |
 | concentración de masa del componente  |
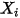 | fracción molar del componente  |
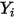 | fracción másica del componente  |
Las cuatro cantidades se relacionan de la siguiente manera:
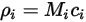
Ecuación 2.314
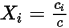
Ecuación 2.315
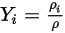
Ecuación 2.316
donde,
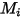 | peso molecular del componente  |
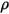 | densidad de la mezcla |
 | suma de las concentraciones molares de todos los componentes de un sistema: |
y

Ecuación 2.317
donde 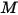 es el peso molecular de la mezcla:
es el peso molecular de la mezcla:
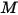 es el peso molecular de la mezcla:
es el peso molecular de la mezcla: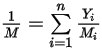
Ecuación 2.318
La ecuación 2.317 indica que, con el peso molecular ponderado de la fracción másica para la mezcla, la ecuación 2.314 también se aplica a la mezcla de los componentes 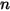 .
.
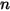 .
.Asimismo, de las definiciones de la ecuación 2.315 y la ecuación 2.316, se deduce que la suma de las fracciones molar y másica deben ser la unidad:
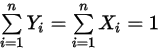
Ecuación 2.319
En solvers CFA, la fracción másica del componente arbitrario 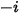 ,
, 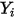 se obtiene directamente mediante la resolución de ecuaciones de transporte diferenciales parciales. Las otras variables,
se obtiene directamente mediante la resolución de ecuaciones de transporte diferenciales parciales. Las otras variables, 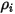 ,
, 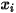 y
y 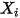 son variables auxiliares que se utilizan para el postproceso.
son variables auxiliares que se utilizan para el postproceso.
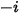 ,
, 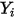 se obtiene directamente mediante la resolución de ecuaciones de transporte diferenciales parciales. Las otras variables,
se obtiene directamente mediante la resolución de ecuaciones de transporte diferenciales parciales. Las otras variables, 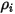 ,
, 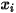 y
y 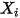 son variables auxiliares que se utilizan para el postproceso.
son variables auxiliares que se utilizan para el postproceso.Ecuaciones gobernantes
En un flujo multicomponente, el movimiento en masa de la mezcla se modela mediante los campos de velocidad única, presión, temperatura y turbulencia. Para la mezcla y el transporte de especies químicas, cada componente tiene su propia ecuación gobernante para la conservación de masa. La influencia de varios componentes en el flujo en masa se percibe a través de la variación de las propiedades de la mezcla, como la densidad, la viscosidad, con las propiedades del componente y las fracciones másicas locales.
• Ecuaciones de fracción másica
Para el flujo de mezcla de componentes 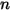 , si no hay reacciones químicas, el transporte de un componente arbitrario
, si no hay reacciones químicas, el transporte de un componente arbitrario  se rige por la siguiente ecuación:
se rige por la siguiente ecuación:
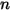 , si no hay reacciones químicas, el transporte de un componente arbitrario
, si no hay reacciones químicas, el transporte de un componente arbitrario  se rige por la siguiente ecuación:
se rige por la siguiente ecuación: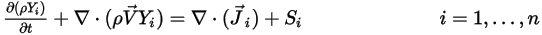
Ecuación 2.320
donde,
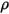 y y  | densidad y velocidad de la mezcla |
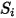 | cualquier origen definido por el usuario |
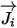 | término de difusión másica |
Para flujos laminares, el vector de velocidad 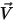 y la fracción másica
y la fracción másica 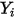 son variables instantáneas. Para flujos turbulentos, estos vectores de velocidad son cantidades a las que se ha aplicado el promedio de Favre, ya que los flujos multicomponente se consideran como densidad variable o flujos comprimibles.
son variables instantáneas. Para flujos turbulentos, estos vectores de velocidad son cantidades a las que se ha aplicado el promedio de Favre, ya que los flujos multicomponente se consideran como densidad variable o flujos comprimibles.
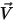 y la fracción másica
y la fracción másica 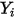 son variables instantáneas. Para flujos turbulentos, estos vectores de velocidad son cantidades a las que se ha aplicado el promedio de Favre, ya que los flujos multicomponente se consideran como densidad variable o flujos comprimibles.
son variables instantáneas. Para flujos turbulentos, estos vectores de velocidad son cantidades a las que se ha aplicado el promedio de Favre, ya que los flujos multicomponente se consideran como densidad variable o flujos comprimibles.En la ecuación 2.320, las cantidades de la mezcla y el término de difusión másica se definen de la siguiente manera:
◦ Densidad de la mezcla: valor medio de masa de todas las densidades de componentes.
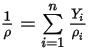
Ecuación 2.321
Para una mezcla de especies gaseosas, la densidad de la mezcla se calcula mediante la ley de gas ideal basada en el peso molecular de la mezcla  , que se calcula mediante la ecuación 2.318:
, que se calcula mediante la ecuación 2.318:
 , que se calcula mediante la ecuación 2.318:
, que se calcula mediante la ecuación 2.318: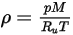
Ecuación 2.322
donde,
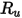 | Constante de gas universal |
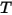 | temperatura de la mezcla |
 | presión absoluta |
Si se utiliza la presión operativa (constante), la ecuación 2.322 se reduce a la denominada ley de gas ideal no comprimible. Es una suposición adecuada para la mezcla y el transporte de especies, donde la presión del indicador es a menudo despreciable en comparación con la presión operativa.
◦ Velocidad de la mezcla: el valor medio de la masa de todas las velocidades de componentes.
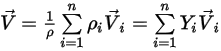
Ecuación 2.323
Sin embargo, dado que solo se resuelve una única velocidad, se supone que la velocidad de la mezcla y todas las velocidades de componente tienen los mismos valores.
◦ Flujo de difusión másica: el flujo de difusión másica del componente  consta de dos partes; los términos de difusión laminar y turbulenta, que se expresan como:
consta de dos partes; los términos de difusión laminar y turbulenta, que se expresan como:
 consta de dos partes; los términos de difusión laminar y turbulenta, que se expresan como:
consta de dos partes; los términos de difusión laminar y turbulenta, que se expresan como:
Ecuación 2.324
En la ecuación 2.324, 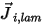 es el flujo de difusión laminar del componente
es el flujo de difusión laminar del componente  que surge debido a los gradientes de concentración y temperatura. Por defecto, Creo Flow Analysis utiliza la aproximación de dilución o ley de Flick para modelar la difusión másica debido a los gradientes de concentración. El flujo de difusión laminar tiene la siguiente formulación:
que surge debido a los gradientes de concentración y temperatura. Por defecto, Creo Flow Analysis utiliza la aproximación de dilución o ley de Flick para modelar la difusión másica debido a los gradientes de concentración. El flujo de difusión laminar tiene la siguiente formulación:
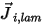 es el flujo de difusión laminar del componente
es el flujo de difusión laminar del componente  que surge debido a los gradientes de concentración y temperatura. Por defecto, Creo Flow Analysis utiliza la aproximación de dilución o ley de Flick para modelar la difusión másica debido a los gradientes de concentración. El flujo de difusión laminar tiene la siguiente formulación:
que surge debido a los gradientes de concentración y temperatura. Por defecto, Creo Flow Analysis utiliza la aproximación de dilución o ley de Flick para modelar la difusión másica debido a los gradientes de concentración. El flujo de difusión laminar tiene la siguiente formulación: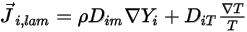
Ecuación 2.325
donde 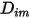 es el coeficiente de difusión másica para el componente
es el coeficiente de difusión másica para el componente  en la mezcla y
en la mezcla y 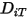 es el coeficiente de difusión térmica (Soret).
es el coeficiente de difusión térmica (Soret).
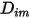 es el coeficiente de difusión másica para el componente
es el coeficiente de difusión másica para el componente  en la mezcla y
en la mezcla y 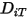 es el coeficiente de difusión térmica (Soret).
es el coeficiente de difusión térmica (Soret).Para flujos turbulentos, el término fluctuante derivado del promedio de Favre de la advección de la ecuación 2.320 se modela como difusión turbulenta:
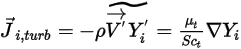
Ecuación 2.326
donde,
 | viscosidad turbulenta |
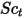 | número de Schmidt turbulento 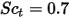 por defecto por defecto |
La difusión turbulenta suele sobrecargar la difusión laminar. La especificación de propiedades detalladas de difusión laminar en los flujos turbulentos suele ser menos importante que la contrapartida turbulenta.
Para derivar la ecuación de continuidad de masa para el flujo de la mezcla, añada todas las ecuaciones de fracción másica del componente y aplique la ecuación 2.319:
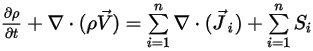
Ecuación 2.327
Para satisfacer la conservación de masa total del flujo de la mezcla, la suma de los términos de difusión de todos los componentes debe ser cero,
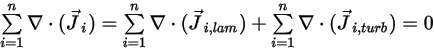
Ecuación 2.328
De la ecuación 2.319 y la ecuación 2.326, se deduce que el término de difusión turbulenta siempre se determina en cero. Por lo tanto, para los flujos completamente turbulentos, se suele considerar que la ecuación 2.328 se satisface automáticamente. Sin embargo, para los flujos laminares o cuando no se puede desestimar la difusión másica laminar en flujos turbulentos, la ecuación 2.328 se reduce a la forma siguiente:

Ecuación 2.329
A continuación, para satisfacer la ecuación 2.329, se aplican las dos restricciones independientes:
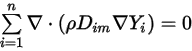
Ecuación 2.330
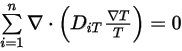
Ecuación 2.331
La ecuación de continuidad de los flujos multicomponente tiene la forma final:
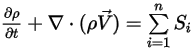
Ecuación 2.332
• Coeficientes de difusión
Para resolver la ecuación 2.320 de transporte para flujos laminares multicomponente, se requiere el coeficiente de difusión másica 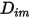 y el coeficiente de difusión térmica
y el coeficiente de difusión térmica 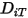 para cada componente de una mezcla. Los métodos para determinar
para cada componente de una mezcla. Los métodos para determinar 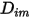 y
y 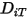 son los siguientes:
son los siguientes:
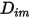 y el coeficiente de difusión térmica
y el coeficiente de difusión térmica 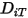 para cada componente de una mezcla. Los métodos para determinar
para cada componente de una mezcla. Los métodos para determinar 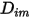 y
y 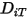 son los siguientes:
son los siguientes:◦ Coeficientes de difusión másica: la formulación del flujo de difusión másica en flujos laminares, la ecuación 2.325, es absolutamente válida cuando la composición de la mezcla no cambia, o cuando 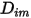 es independiente de la composición. Se trata de una aproximación aceptable en las mezclas diluidas cuando
es independiente de la composición. Se trata de una aproximación aceptable en las mezclas diluidas cuando  es muy pequeña para todos los componentes, excepto para el gas portador. Para las mezclas no diluidas en flujos laminares multicomponente,
es muy pequeña para todos los componentes, excepto para el gas portador. Para las mezclas no diluidas en flujos laminares multicomponente, 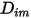 se calcula a partir de la siguiente formulación:
se calcula a partir de la siguiente formulación:
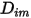 es independiente de la composición. Se trata de una aproximación aceptable en las mezclas diluidas cuando
es independiente de la composición. Se trata de una aproximación aceptable en las mezclas diluidas cuando  es muy pequeña para todos los componentes, excepto para el gas portador. Para las mezclas no diluidas en flujos laminares multicomponente,
es muy pequeña para todos los componentes, excepto para el gas portador. Para las mezclas no diluidas en flujos laminares multicomponente, 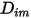 se calcula a partir de la siguiente formulación:
se calcula a partir de la siguiente formulación:
Ecuación 2.333
donde  es el coeficiente de difusión másica binario del componente
es el coeficiente de difusión másica binario del componente  en
en  , que se debe especificar o calcular.
, que se debe especificar o calcular.
 es el coeficiente de difusión másica binario del componente
es el coeficiente de difusión másica binario del componente  en
en  , que se debe especificar o calcular.
, que se debe especificar o calcular.◦ Valor especificado: el coeficiente de difusión másica binario 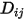 es una constante o función de temperatura si se tiene en cuenta la transferencia de calor. El valor se puede especificar directamente u obtenerse del número de Schmidt especificado:
es una constante o función de temperatura si se tiene en cuenta la transferencia de calor. El valor se puede especificar directamente u obtenerse del número de Schmidt especificado:
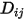 es una constante o función de temperatura si se tiene en cuenta la transferencia de calor. El valor se puede especificar directamente u obtenerse del número de Schmidt especificado:
es una constante o función de temperatura si se tiene en cuenta la transferencia de calor. El valor se puede especificar directamente u obtenerse del número de Schmidt especificado: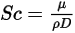
Ecuación 2.334
donde,
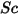 | Número de Schmidt |
El número de Schmidt se define como la relación de la velocidad de difusión viscosa con respecto a la velocidad de difusión molecular (masa).
Si se aplica un valor o una función de temperatura para todos los componentes, la ecuación 2.333 se reduce a
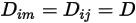
Ecuación 2.335
La ecuación 2.335 es una aproximación adecuada para modelar una mezcla diluida, con las especies presentes en fracciones másicas bajas en un fluido de portador que tiene una concentración elevada. En estos casos, 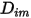 se define directamente como una constante o una función de temperatura.
se define directamente como una constante o una función de temperatura.
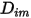 se define directamente como una constante o una función de temperatura.
se define directamente como una constante o una función de temperatura.Sin embargo, para mezclas no diluidas, con 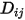 especificado, se utiliza la ecuación 2.333 para calcular el coeficiente de difusión másica individual de la mezcla
especificado, se utiliza la ecuación 2.333 para calcular el coeficiente de difusión másica individual de la mezcla 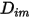 .
.
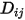 especificado, se utiliza la ecuación 2.333 para calcular el coeficiente de difusión másica individual de la mezcla
especificado, se utiliza la ecuación 2.333 para calcular el coeficiente de difusión másica individual de la mezcla 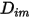 .
.◦ Teoría cinética: para un gas ideal, el coeficiente de difusión másica binaria 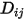 también se puede obtener mediante la teoría cinética.
también se puede obtener mediante la teoría cinética.
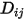 también se puede obtener mediante la teoría cinética.
también se puede obtener mediante la teoría cinética.Referencias: H. A. McGee, "Molecular Engineering", McGraw-Hill, New York, 1991.
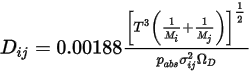
Ecuación 2.336
donde 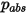 es la presión absoluta y
es la presión absoluta y 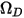 es la integral de colisión de difusión, que es una medida de la interacción de las moléculas en el sistema.
es la integral de colisión de difusión, que es una medida de la interacción de las moléculas en el sistema.  es una función de la cantidad
es una función de la cantidad 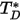 , definida como:
, definida como:
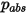 es la presión absoluta y
es la presión absoluta y 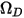 es la integral de colisión de difusión, que es una medida de la interacción de las moléculas en el sistema.
es la integral de colisión de difusión, que es una medida de la interacción de las moléculas en el sistema.  es una función de la cantidad
es una función de la cantidad 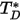 , definida como:
, definida como: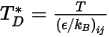
Ecuación 2.337
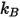 es la constante de Boltzmann, que se define como la constante de gas universal
es la constante de Boltzmann, que se define como la constante de gas universal  dividida por el número de Avogadro.
dividida por el número de Avogadro. 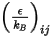 para la mezcla es la media geométrica:
para la mezcla es la media geométrica: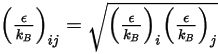
Ecuación 2.338
Para una mezcla binaria, 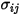 se calcula como la media aritmética de
se calcula como la media aritmética de 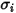 y
y 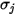 individuales:
individuales:
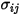 se calcula como la media aritmética de
se calcula como la media aritmética de 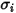 y
y 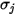 individuales:
individuales:
Ecuación 2.339
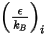 y
y 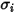 son los parámetros de Lennard-Jones para el componente
son los parámetros de Lennard-Jones para el componente  en la mezcla. Concretamente,
en la mezcla. Concretamente,  es el corte transversal de colisión de la molécula de esfera con el diámetro
es el corte transversal de colisión de la molécula de esfera con el diámetro 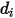 (se debe tener en cuenta que una molécula barre un área determinada el doble de su diámetro, ya que las moléculas con las que colisiona también tienen diámetro
(se debe tener en cuenta que una molécula barre un área determinada el doble de su diámetro, ya que las moléculas con las que colisiona también tienen diámetro 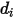 ); y
); y 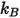 = 1.38064852(79) × 10-23(J/K) es la constante de Boltzmann.
= 1.38064852(79) × 10-23(J/K) es la constante de Boltzmann.En Creo Flow Analysis, el diámetro 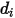 y la energía
y la energía 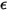 se especifican para determinar los dos parámetros de Lennard-Jones.
se especifican para determinar los dos parámetros de Lennard-Jones.
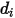 y la energía
y la energía 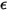 se especifican para determinar los dos parámetros de Lennard-Jones.
se especifican para determinar los dos parámetros de Lennard-Jones.◦ Coeficientes de difusión térmica 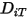 : los coeficientes de difusión térmica se pueden definir como constantes, funciones polinomiales de temperatura, funciones definidas por el usuario o bien mediante la siguiente expresión dependiente de la composición con base empírica, derivada de lo siguiente.
: los coeficientes de difusión térmica se pueden definir como constantes, funciones polinomiales de temperatura, funciones definidas por el usuario o bien mediante la siguiente expresión dependiente de la composición con base empírica, derivada de lo siguiente.
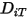 : los coeficientes de difusión térmica se pueden definir como constantes, funciones polinomiales de temperatura, funciones definidas por el usuario o bien mediante la siguiente expresión dependiente de la composición con base empírica, derivada de lo siguiente.
: los coeficientes de difusión térmica se pueden definir como constantes, funciones polinomiales de temperatura, funciones definidas por el usuario o bien mediante la siguiente expresión dependiente de la composición con base empírica, derivada de lo siguiente.Referencias: K. K. Y. Kuo, "Principles of Combustion", John Wiley and Sons, New York, 1986.
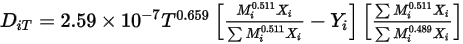
Ecuación 2.340
Esta forma del coeficiente de difusión térmica hace que las moléculas pesadas se difundan menos rápidamente y las moléculas ligeras se difundan con más rapidez, hacia las superficies calentadas.
• Ecuaciones de momento
Con las propiedades de masa ponderada y las velocidades, las ecuaciones de momento para la mezcla de todos los componentes tienen la misma expresión que las de los flujos de fluido único:
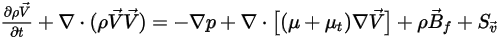
Ecuación 2.341
donde la densidad de la mezcla y la velocidad se calculan mediante la ecuación 2.321, la ecuación 2.322 y la ecuación 2.323. La viscosidad turbulenta se calcula directamente a partir de los modelos de turbulencia basados en el flujo de la mezcla, de modo que su valor es independiente de los componentes. Para la viscosidad laminar, se calcula de la siguiente manera:
◦ Viscosidad laminar de masa media: para mezclas de gas no ideales, la viscosidad de la mezcla se calcula en función de una fracción de masa media de las viscosidades de las especies químicas puras (componentes):
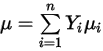
Ecuación 2.342
◦ Teoría cinética: en el caso de las mezclas de gases ideales, la viscosidad de la mezcla se calcula en función de la teoría cinética. Para cada componente, la viscosidad dinámica se basa en la ecuación de Boltzmann:
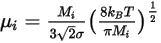
Ecuación 2.343
Para la difusividad másica, se requieren los parámetros de Lennard-Jones, 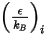 y
y  , para calcular las viscosidades de los componentes de gas en una mezcla.
, para calcular las viscosidades de los componentes de gas en una mezcla.
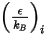 y
y  , para calcular las viscosidades de los componentes de gas en una mezcla.
, para calcular las viscosidades de los componentes de gas en una mezcla.La viscosidad para la mezcla de gas ideal se calcula de la siguiente manera:
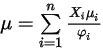
Ecuación 2.344
donde,

Ecuación 2.345
• Ecuación de energía
Tal como se describe en el módulo Calor (Heat), la ecuación de energía para la mezcla de todos los componentes se expresa de la siguiente manera:

Ecuación 2.346
donde 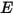 y
y 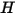 son la energía interna total y la entalpía total de la mezcla de componentes
son la energía interna total y la entalpía total de la mezcla de componentes 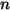 . Junto con el calor específico de la mezcla
. Junto con el calor específico de la mezcla 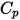 y la entalpía estática
y la entalpía estática 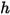 , se obtienen calculando la media de masa de los valores correspondientes de cada componente:
, se obtienen calculando la media de masa de los valores correspondientes de cada componente:
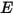 y
y 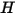 son la energía interna total y la entalpía total de la mezcla de componentes
son la energía interna total y la entalpía total de la mezcla de componentes 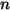 . Junto con el calor específico de la mezcla
. Junto con el calor específico de la mezcla 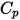 y la entalpía estática
y la entalpía estática 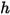 , se obtienen calculando la media de masa de los valores correspondientes de cada componente:
, se obtienen calculando la media de masa de los valores correspondientes de cada componente:◦ Capacidad calorífica de la mezcla de masa media
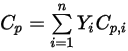
Ecuación 2.347
◦ Masa: energía y entalpía promedio de la mezcla
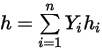
Ecuación 2.348
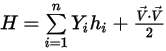
Ecuación 2.349
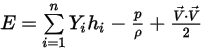
Ecuación 2.350
La entalpía estática de un componente consta de dos partes: la entalpía de referencia y la entalpía sensible del estado estándar. Para los flujos multicomponente, se incluyen ambas partes de la entalpía (valor absoluto o total) al calcular 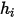 .
.
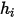 .
.En la ecuación 2.336, el primer término del lado derecho representa la difusión de la energía. Consta de tres partes: conducción del calor, transporte de energía debido a la difusión de las especies y calentamiento viscoso. Para la conducción de calor de la mezcla, se modela de la misma manera que en el flujo de fluido único. En Creo Flow Analysis, la conductividad de calor de la mezcla se calcula de la siguiente manera:
◦ Conductividad de calor de masa media: en el caso de las mezclas de gases no ideales, la conductividad de calor de la mezcla se calcula en función de una fracción másica media simple de las conductividades de calor de especies o componentes puros.
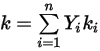
Ecuación 2.351
Es el método por defecto en Creo Flow Analysis.
◦ Teoría cinética: en el caso de las mezclas de gases ideales, la conductividad de calor de la mezcla se puede calcular según la teoría cinética. Para cada componente, la conductividad de calor tiene la forma:

Ecuación 2.352
donde,
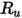 | Constante de gas universal |
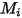 | Peso molecular |
 | viscosidad especificada o calculada del componente |
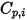 | capacidad calorífica específica calculada o especificada del componente |
Se debe tener en cuenta que, igual que la viscosidad laminar, 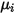 , el calor específico
, el calor específico 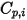 también se puede obtener con la teoría cinética:
también se puede obtener con la teoría cinética:
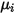 , el calor específico
, el calor específico 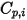 también se puede obtener con la teoría cinética:
también se puede obtener con la teoría cinética: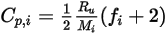
Ecuación 2.353
donde  es el número de modos de almacenamiento de energía (grados de libertad de movimiento) para el componente de gas
es el número de modos de almacenamiento de energía (grados de libertad de movimiento) para el componente de gas  .
.
 es el número de modos de almacenamiento de energía (grados de libertad de movimiento) para el componente de gas
es el número de modos de almacenamiento de energía (grados de libertad de movimiento) para el componente de gas  .
.La conductividad de calor para la mezcla de gas ideal se calcula de la siguiente manera:
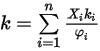
Ecuación 2.354
donde 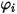 se expresa en la ecuación 2.335.
se expresa en la ecuación 2.335.
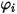 se expresa en la ecuación 2.335.
se expresa en la ecuación 2.335.El segundo término de difusión,
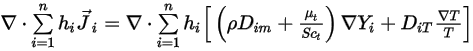
Ecuación 2.355
representa el transporte de entalpía debido a la difusión de las especies químicas en el flujo de componentes 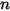 . Este término puede tener un efecto significativo en el campo de entalpía y no debe descuidarse. Cuando el número de Lewis, la relación de la difusividad térmica
. Este término puede tener un efecto significativo en el campo de entalpía y no debe descuidarse. Cuando el número de Lewis, la relación de la difusividad térmica 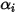 con respecto a la difusividad másica
con respecto a la difusividad másica 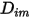 :
:
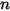 . Este término puede tener un efecto significativo en el campo de entalpía y no debe descuidarse. Cuando el número de Lewis, la relación de la difusividad térmica
. Este término puede tener un efecto significativo en el campo de entalpía y no debe descuidarse. Cuando el número de Lewis, la relación de la difusividad térmica 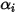 con respecto a la difusividad másica
con respecto a la difusividad másica 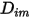 :
:
Ecuación 2.356
para cualquier especie no sea unidad, el descuido de este término puede provocar errores significativos.
El tercer término de difusión es la contribución de calentamiento viscoso  . Aunque se trate del mismo modo que en el flujo de fluido único, la cizalla
. Aunque se trate del mismo modo que en el flujo de fluido único, la cizalla 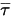 se calcula con las viscosidades laminar y turbulenta de la mezcla. El término de origen general
se calcula con las viscosidades laminar y turbulenta de la mezcla. El término de origen general 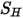 es el origen de calor externo o del usuario total en todos los componentes.
es el origen de calor externo o del usuario total en todos los componentes.
 . Aunque se trate del mismo modo que en el flujo de fluido único, la cizalla
. Aunque se trate del mismo modo que en el flujo de fluido único, la cizalla 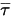 se calcula con las viscosidades laminar y turbulenta de la mezcla. El término de origen general
se calcula con las viscosidades laminar y turbulenta de la mezcla. El término de origen general 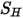 es el origen de calor externo o del usuario total en todos los componentes.
es el origen de calor externo o del usuario total en todos los componentes.• Modelos de turbulencia: con la densidad de la mezcla 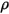 , la viscosidad molecular
, la viscosidad molecular 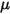 y la velocidad
y la velocidad 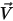 , las ecuaciones de modelado de turbulencias en los modelos estándar k-ε y RNG k-ε tienen las mismas formas generales que en los modelos de turbulencia de un solo fluido. Se describen en el módulo Turbulencia (Turbulence). La viscosidad turbulenta para la mezcla
, las ecuaciones de modelado de turbulencias en los modelos estándar k-ε y RNG k-ε tienen las mismas formas generales que en los modelos de turbulencia de un solo fluido. Se describen en el módulo Turbulencia (Turbulence). La viscosidad turbulenta para la mezcla 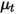 se calcula directamente con la expresión:
se calcula directamente con la expresión:
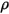 , la viscosidad molecular
, la viscosidad molecular 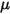 y la velocidad
y la velocidad 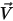 , las ecuaciones de modelado de turbulencias en los modelos estándar k-ε y RNG k-ε tienen las mismas formas generales que en los modelos de turbulencia de un solo fluido. Se describen en el módulo Turbulencia (Turbulence). La viscosidad turbulenta para la mezcla
, las ecuaciones de modelado de turbulencias en los modelos estándar k-ε y RNG k-ε tienen las mismas formas generales que en los modelos de turbulencia de un solo fluido. Se describen en el módulo Turbulencia (Turbulence). La viscosidad turbulenta para la mezcla 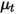 se calcula directamente con la expresión:
se calcula directamente con la expresión: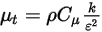
Ecuación 2.357
Además, la producción de energía cinética turbulenta se calcula en función de los gradientes de viscosidad y velocidad turbulentas de la mezcla:
Modelado de límites multicomponente
En un flujo multicomponente, las condiciones de límite para las ecuaciones de modelado del flujo, la energía y la turbulencia son las mismas que las de los flujos de una sola fase descritos en los módulos Flujo (Flow), Calor (Heat) y Turbulencia (Turbulence). Para las fracciones másicas de un componente, las condiciones de límite constan de un valor especificado, un flujo volumétrico especificado y/o un gradiente.
• Límite de entrada de componente n
En un límite de entrada, el transporte neto de un componente puede estar formado por contribuciones de convección y de difusión. La convección viene determinada por la fracción másica de las especies de entrada especificadas. La difusión depende del gradiente del campo de fracción másica calculada. En las velocidades muy pequeñas de entrada convectiva, se puede ganar o perder masa sustancial a través de la entrada debido a la difusión. Por este motivo, la difusión de entrada no se incluye por defecto, pero se puede activar como opción.
◦ Valor especificado: para el flujo de componentes 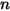 , las fracciones másicas de entrada se determinan previamente para los componentes
, las fracciones másicas de entrada se determinan previamente para los componentes 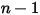 , mientras que la fracción másica del componente
, mientras que la fracción másica del componente 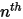 se obtiene utilizando la ecuación 2.319 de restricción física.
se obtiene utilizando la ecuación 2.319 de restricción física.
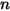 , las fracciones másicas de entrada se determinan previamente para los componentes
, las fracciones másicas de entrada se determinan previamente para los componentes 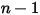 , mientras que la fracción másica del componente
, mientras que la fracción másica del componente 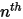 se obtiene utilizando la ecuación 2.319 de restricción física.
se obtiene utilizando la ecuación 2.319 de restricción física.
Ecuación 2.358
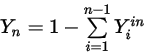
Ecuación 2.359
Asimismo, la fracción másica de cada componente no debe ser negativa.
◦ Flujo volumétrico especificado: suponiendo que 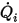 es el flujo volumétrico de entrada descrito anteriormente para el componente
es el flujo volumétrico de entrada descrito anteriormente para el componente  , se dispone de un flujo másico de cada componente
, se dispone de un flujo másico de cada componente 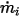 y el flujo másico total en la entrada
y el flujo másico total en la entrada 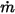 del modo que se indica a continuación.
del modo que se indica a continuación.
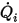 es el flujo volumétrico de entrada descrito anteriormente para el componente
es el flujo volumétrico de entrada descrito anteriormente para el componente  , se dispone de un flujo másico de cada componente
, se dispone de un flujo másico de cada componente 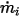 y el flujo másico total en la entrada
y el flujo másico total en la entrada 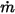 del modo que se indica a continuación.
del modo que se indica a continuación.
Ecuación 2.360
donde 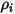 es la densidad de entrada del componente
es la densidad de entrada del componente  .
.
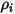 es la densidad de entrada del componente
es la densidad de entrada del componente  .
.Por definición, la fracción de masa se calcula de la siguiente manera:
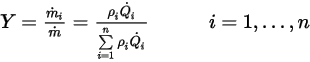
Ecuación 2.361
◦ Límite de salida, simetría, de pared: para los componentes 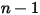 , se aplican las condiciones de gradiente cero para todos los límites de salida, simetría y pared, mientras que la fase
, se aplican las condiciones de gradiente cero para todos los límites de salida, simetría y pared, mientras que la fase  se obtiene mediante la restricción física.
se obtiene mediante la restricción física.
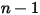 , se aplican las condiciones de gradiente cero para todos los límites de salida, simetría y pared, mientras que la fase
, se aplican las condiciones de gradiente cero para todos los límites de salida, simetría y pared, mientras que la fase  se obtiene mediante la restricción física.
se obtiene mediante la restricción física.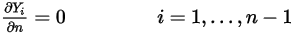
Ecuación 2.362
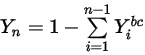
Ecuación 2.363
donde 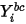 es el valor de límite obtenido de la ecuación 2.347.
es el valor de límite obtenido de la ecuación 2.347.
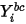 es el valor de límite obtenido de la ecuación 2.347.
es el valor de límite obtenido de la ecuación 2.347.Consideraciones numéricas
Las ecuaciones gobernantes, los modelos de turbulencia y las condiciones de límite anteriores constituyen la base del modelo de mezcla multicomponente. Sin términos de origen externo o de usuario ni reacciones químicas, se trata de un sistema de ecuaciones cerrado que se resuelve numéricamente mediante un solver de volumen finito basado en la presión.
Se resuelven las ecuaciones de transporte de fracciones másicas para todos los componentes. Para satisfacer la restricción física, las fracciones másicas reales se escalan según la suma de los valores resueltos para todos los componentes:

Ecuación 2.364
donde 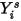 es el valor obtenido al resolver la ecuación 2.320. La fracción másica real es:
es el valor obtenido al resolver la ecuación 2.320. La fracción másica real es:
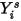 es el valor obtenido al resolver la ecuación 2.320. La fracción másica real es:
es el valor obtenido al resolver la ecuación 2.320. La fracción másica real es: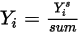
Ecuación 2.365