Bénéfice de la symétrie plane
La symétrie permet d'analyser une seule portion d'une géométrie. Ceci représente un gros avantage sur les temps de calcul et les besoins en ressources. Elle permet également d'éliminer les mouvements de corps rigides. Outre la géométrie, les propriétés, les charges et les restrictions attribuées au modèle doivent être symétriques.
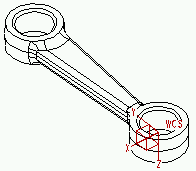
• Restrictions : pour la symétrie plane ou miroir, contraignez tous les degrés de liberté qui permettent la déformation dans le plan de la symétrie. L'exemple suivant montre comment un modèle peut être approximé par un quart de section à l'aide d'une symétrie plane :
Modèle complet
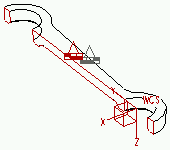
a
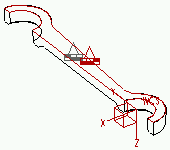
b
Dx, Ry et Rz sont fixes dans a, et Dz, Rx et Ry sont fixes dans b. Notez que les éléments solides ne comportent pas de degrés de liberté en rotation et qu'il n'est donc pas nécessaire de restreindre Rx, Ry et Rz.
• Restrictions dans Thermal : les modèles Thermal exigent des conditions de symétrie, mais celles-ci existent déjà par défaut. Aucune restriction dans Thermal n'implique que la frontière est un isolant parfait (la chaleur ne traverse pas le plan de symétrie).
• Charges : dans les modèles de symétrie, le chargement doit également être symétrique. Dans certains cas, vous devez réduire l'intensité des charges autant de fois que la géométrie a de symétries. Par exemple, lorsque vous analysez une moitié de section, vous devez également diminuer certaines charges de type palier. En règle générale, vous devez échelonner les charges totales (charges totales de
point, de
courbe et de surface,
charges totales appliquées en un point,
charges totales de type palier appliquées en un point,
charges de type palier et
charges totales thermiques). Les charges qui sont une fonction de surface (
pression,
charge thermique par unité,
force par surface unitaire) ou de volume (
charges centrifuges,
gravité,
charges thermiques volumétriques) n'ont pas besoin d'être mises à l'échelle.
• Propriétés : en règle générale, seules les propriétés de matériau isotropes doivent être utilisées pour la symétrie, sauf si les orientations d'un matériau anisotrope sont en réalité symétriques.