Дифференциальные уравнения в частных производных в блоках решения
pdesolve(u, x, xrange, t, trange, [xpts], [tpts]) - возвращает функцию или вектор функций u(x,t), который решает одномерное нелинейное дифференциальное уравнение в частных производных (ДУЧП) или систему ДУЧП с n независимыми ограничениями равенства для дифференциального уравнения n-го порядка. Значения интерполируются из матрицы точек решения, рассчитанных с помощью численного метода линий.
Необходимо использовать pdesolve в блоке решения.
Аргументы
• u представляет имя скалярной функции или вектор имени функции (без включения имен переменных) в том виде, в каком они появляются в блоке решения. Например, если выполняется решение для функций f(x,t) и g(x,t), u будет иметь следующий вид:
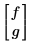
Чтобы использовать нотацию нижних индексов в частных производных, нельзя использовать литералы в нижних индексах при именовании функций.
• x - имя переменной времени.
• xrange- двухэлементный вектор-столбец, содержащий вещественные граничные значения для x.
• t - имя переменной времени.
• trange- двухэлементный вектор-столбец, содержащий вещественные граничные значения для t.
• xpts (необязательно) - целое число точек пространственной дискретизации.
• tpts (необязательно) - целое число точек временной дискретизации.
Применяются общие правила определения блока решения. В теле блока:
Неизвестные функции
Функции должны быть определены со своими переменными. Например, используйте u(x,t), а не u. Чтобы указать частичную производную в блоке решения, используйте одну из следующих возможностей:
• Нотация с нижними индексами. Например, uxx(x,t) является второй частной производной u по x.
Нотация с нижними индексами может использоваться только в блоках решения pdesolve и не может использоваться в других областях документа. |
Уравнения в частных производных
Уравнения должны быть определены с помощью логического равенства. Вторые частные производные не разрешены в левой части уравнений. Уравнение необходимо преобразовать в систему уравнений в частных производных только первого порядка.
Граничные условия
Для каждой неизвестной функции должны существовать начальное условие u(x,0) и n граничных условий, где n - это порядок ДУЧП. Граничные условия могут иметь тип Дирихле (u(0,t) = f(t)) или Неймана (ux(0,t)=g(t)) и могут быть заданы в любой конечной точке пространственного диапазона интегрирования. Конечные точки, используемые в граничных условиях, должны соответствовать конечным точкам, указанным в команде ode/pdesolve. Mathcad проверяет правильность типа и количества ограничений и помечает ошибки с сообщением об ошибке.
Зависимости
Допускаются алгебраические ограничения вида u(x,t)+v(x,t)+w(x,t)=0. При этом в систему добавляется дополнительная неизвестная функция w, которая должна быть указана как одна из выходных функций в вызове ode/pdesolve. Ограничения в виде неравенства не допускаются.
• Назначьте выходным данным функции pdesolve имя функции или вектор имен функций.
• Чтобы изменить метод аппроксимации, используемый для частных производных, щелкните правой кнопкой мыши функцию pdesolve и выберите другой метод. Это может повлиять на время расчета.
• Численный метод линий подходит только для решения гиперболических и параболических ДУЧП и алгебраических уравнений с частными производными. Для решения уравнения в программном цикле используйте numol. Для решения эллиптических ДУЧП, таких как уравнение Пуассона, используйте методы Relax или Multigrid.
Ниже перечисляются возможные ошибки и решения при работе с pdesolve.
• Ошибка. This function requires at least 5 arguments but is applied to 4 (Для этой функции требуется не меньше 5 аргументов, но применяется не более 4).
Пример:
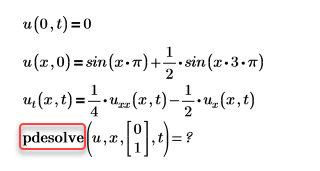
Решение. Добавьте отсутствующие аргументы, в данном случае это trange.
• Ошибка: Эта функция допускает не более 7 аргументов, но применяется она к 8 (This function accepts at most 7 arguments but is applied to 8).
Пример:
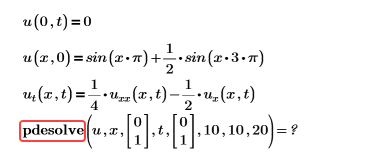
Решение. Удалите ненужные аргументы. См. дополнительные сведения об аргументах.
• Ошибка. Malformed vector of boundaries for time variable (Неверно сформирован вектор границ для переменной времени).
Пример:
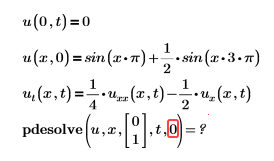
Решение: неверно определяется trange. Дополнительные сведения см. в разделе Аргументы.
• Ошибка. Malformed vector of boundaries for time variable (Неверно сформирован вектор границ для пространственной переменной).
Пример:
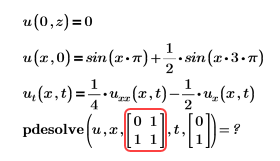
Решение: неверно определяется xrange. Дополнительные сведения см. в разделе Аргументы.
• Ошибка. Unknown function name incorrectly specified (Неверно указано имя неизвестной функции).
Пример:
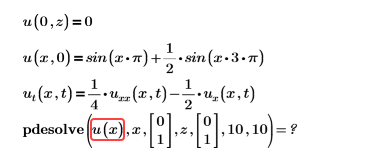
Решение. Функция должна отображаться без аргумента.
• Ошибка: Это значение должно быть целым числом больше 4 (This value must be an integer greater than 4).
Пример:
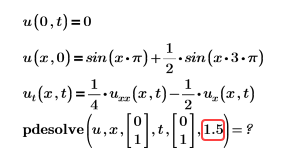
Или
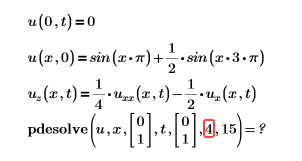
Решение. Число точек дискретизации должно быть целым числом больше 4.