Метод релаксации для решения дифференциальных уравнений в частных производных
• relax(A, B, C, D, E, S, U, rjac)
• multigrid(M, ncycle)
Возвращает квадратную матрицу, в которой положение элемента соответствует его положению внутри квадратной области, а значение элемента приближается к значению решения уравнения в частных производных Пуассона
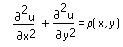
в этой точке. Функция relax решает уравнение Пуассона, используя модифицированный метод Гаусса-Зейделя с последующей верхней релаксацией по сетке.
Функция multigrid применяется в частных случаях, когда все граничные условия переходят в U нулевые. При этом используется метод multigrid.
• Если граничные условия постоянны и равны на всех четырех сторонах, приведите уравнение к нулевым граничным условиям на всех сторонах и воспользуйтесь функцией multigrid, так как она работает быстрее и ее легче настроить.
• В случае ρ = 0 уравнение Пуассона упрощается до уравнения Лапласа.
• При решении гиперболических или параболических ДУЧП или систем ДУЧП используйте функцию numol.
Аргументы
• A, B, C, D, E — квадратные матрицы одинакового размера, содержащие вещественные коэффициенты дискретизированной аппроксимации Лапласа функции u в четырех соседних точках и точке аппроксимации.
• S — квадратная матрица, содержащая исходный элемент в каждой точке внутри квадрата.
• U — квадратная матрица, содержащая граничные значения вдоль краев области и начальные приближения для решения внутри области.
• rjac - вещественное значение 0 < rjac < 1, спектральный радиус итерации Якоби. Этот параметр управляет сходимостью алгоритма релаксации.
Оптимальное значение rjac зависит от конкретных условий задачи, но для начала можно взять значение r, где n — число точек в каждом направлении сетки:
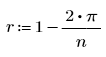
• M — квадратная матрица размером 1 + 2n, элементы которой соответствуют исходным элементам в соответствующих точках квадратной области.
• ncycle — целое число, соответствующее количеству циклов на каждом уровне итерации функции multigrid.
Значение ncycle, равное 2, обычно дает хорошую аппроксимацию решения.