Операторы "производная" и "штрих"
|
Оператор
|
Описание
|
Сочетание клавиш
|
|---|---|---|
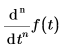 |
Возвращает n-ю производную f(t) по t, вычисляемую в точке t.
• При численном вычислении n - натуральное число между 0 и 5 включительно.
• При аналитическом вычислении n - любое натуральное число.
|
Ctrl+Shift+D
|
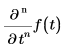 |
Возвращает n-ю частную производную f(t) по t, вычисляемую в точке t.
• При численном вычислении n - натуральное число между 0 и 5 включительно.
• При аналитическом вычислении n - любое натуральное число.
|
Ctrl + D
|
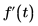 |
Определяет функцию g как 1-ю производную функции f(t).
• Можно расположить каскадом n операторов "штрих", чтобы получить nth производную.
• При численном или аналитическом вычислении можно использовать любое количество операторов "штрих". Однако аналитическое вычисление может занимать намного меньше времени.
|
Ctrl+' (апостроф)
|
Операнды
• f(t) — функция, принимающая скалярные значения. Функция может быть комплексной.
◦ В случае оператора "производная" f(t) может представлять собой функцию любого числа переменных.
◦ В случае оператора "штрих" f(t) должна быть только функцией одной переменной.
• g — имя функции.
• t - точка, в которой вычисляется производная.
Дополнительные сведения
• При вычислении первой производной выражения местозаполнитель степени можно оставить пустым.
• Первая производная вычисляется с точностью до 7—8 значащих цифр при условии, что точка, в которой вычисляется производная, расположена не слишком близко к сингулярности функции. Точность может уменьшаться примерно на 1 значащую цифру за каждое повышение порядка производной.
• Численный метод, используемый при вычислении производных, является разновидностью метода Риддера, в котором вычисляется (n + 1)-точечные разделенные разности с использованием различных размеров шага, где n — порядок производной. Затем с использованием взвешенных средних вычисляются последовательные аппроксимации и сводятся в таблицу. Последовательные записи в таблице сравниваются, и та, у которой оказывается наименьшая ошибка, возвращается как производная при условии, что ошибка не превышает некоторого допустимого уровня.