Пример. Дифференциальные уравнения в частных производных в блоках решения
Используйте дифференциальные уравнения в частных производных (ДУЧП) в блоке решения и решатель дифференциальных уравнений в частных производных numol для сравнения решений волнового уравнения.
Блок решения ДУЧП
Чтобы решить следующее одномерное волновое уравнение:
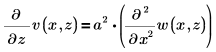
Используйте ограничение:
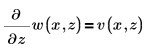
Чтобы создать первое уравнение как систему двух дифференциальных уравнений в частных производных, задайте Блок решения ДУЧП
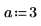
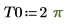
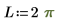
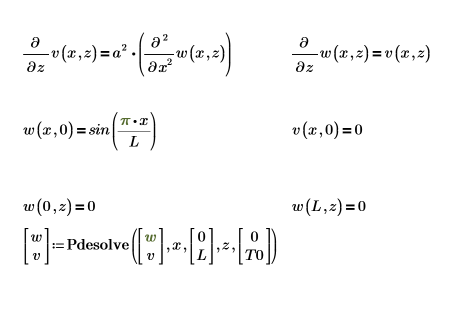
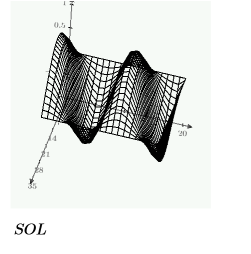
Ниже приведено единственное решение для границы:
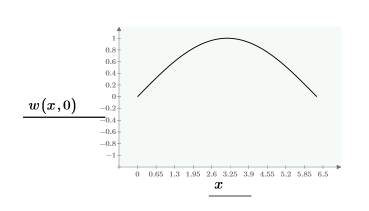
Создайте сетку решений, которые будут отложены на трехмерном графике с помощью функции CreateMesh, используя ограничения, определенные выше:
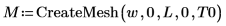
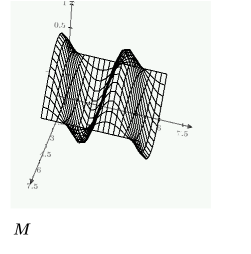
Использование numol
Можно получить решение с помощью решателя командной строки numol. Это особенно полезно, когда требуется включить расчет в программу.
Определите число дифференциальных уравнений в частных производных и алгебраические ограничения в системе:
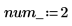
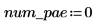
Функция для расчета правой части ДУЧП является вектором длины num_pde + num_pae (алгебраические уравнения в частных производных). В этом случае функция является системой уравнений. Аналогично граничное условие определяется как вектор-столбец длины num_pde + num_pae.
Выражение для вектора ДУЧП:
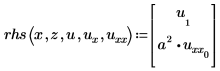
Поэтому u1=v, как определено выше, и u0=w.
Вектор начальных условий:
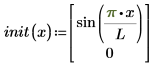
Предположим, что каждая левая сторона является производной по времени первого порядка неизвестного вектора функции u. Переменными функции являются x (пространство) и t (время). Решением является переменная u, которая также может быть вектором решений системы уравнений: ux - первая производная каждого решения u в векторе и uxx - вторая пространственная производная.
Необходимо использовать нижние индексы векторов, чтобы обращаться к отдельным записям в u, ux и uxx.
Вектор граничных условий может содержать три типа строк. Каждая строка определяется одним из следующих элементов:
• rhs содержит пространственные производные второго порядка: требуется два граничных условия ("D" Дирихле или "N" Неймана), по одному для каждой стороны области интегрирования.
• rhs содержит пространственные производные первого порядка: одно граничное условие Дирихле на левой или правой стороне области интегрирования, другое - "Н/Д".
• Если вектор не содержит пространственные производные, граничные условия не требуются.
Граничные условия на левой и правой границах соответствуют следующим условиям.
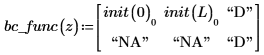
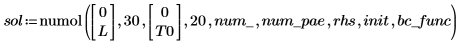
Результатом является матрица numol, представляющая каждую пространственную точку как строку и каждую временную точку как столбец. Это упрощает визуализацию решений, позволяя выбирать по одному столбцу и представлять решение для всего пространства в один момент времени. При решении системы уравнений матрица решения для каждой неизвестной функции добавляется на стороне предыдущей матрицы.
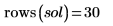
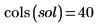
В текущем примере для каждой функции имеется 20 точек времени, поэтому матрица содержит 40 столбцов. Выберем первое решение u0:
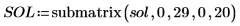
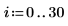
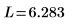
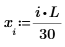
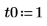
Сравнение numol и Pdesolve
Сравним решения numol и Pdesolve в точке t0:
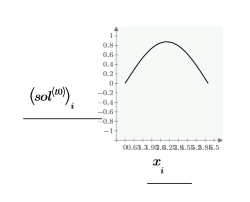
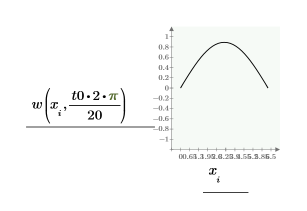
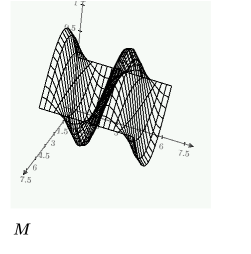
Сравним сетку решений для значений пространства и времени: