Пример. Генераторы шума
Используйте функции whiten, gaussn и onefn для моделирования белого шума, гауссова шума и шума 1/f соответственно.
Белый шум
Функция whiten моделирует шум, создаваемый N независимыми источниками, каждый из которых генерирует случайные числа с равномерным распределением в диапазоне от -0.5 до 0.5.
1. Используйте функцию whiten, чтобы вычислить функцию белого шума для шести независимых источников шума.

Повторное вычисление функции whiten дает другой набор элементов вектора.
2. Вычислите больший выходной вектор.
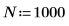
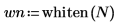
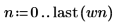
3. Постройте график функции белого шума.
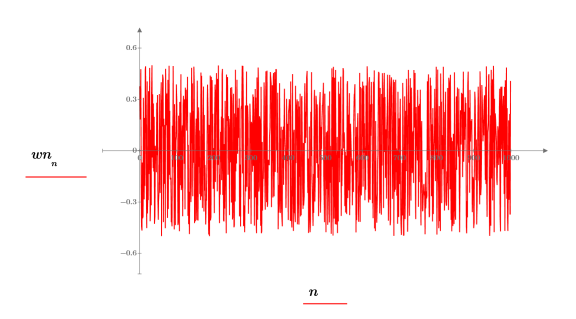
4. Используйте функции mean и stdev, чтобы вычислить среднее и среднеквадратическое отклонение вектора белого шума.
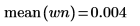
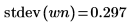
5. Покажите теоретическое значение среднего, а затем используйте функцию var для вычисления среднеквадратического отклонения.
График показывает, что сигнал wn имеет теоретическое среднее, равное 0. | |
Среднеквадратическое отклонение представляет собой квадратный корень из дисперсии. | 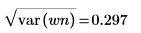 |
6. Сравните рассчитанные значения среднего и среднеквадратического отклонения с теоретическими значениями и убедитесь в отсутствии значительных отклонений.
Гауссов шум
Функция gaussn моделирует x независимых источников шума, удовлетворяющих гауссову распределению вероятностей со средним отклонением 0 и среднеквадратическим отклонением 1.
1. Вычислите функцию гауссова шума, gaussian, для шести независимых источников шума.

Теоретически элементом вектора может быть любое действительное число, но наиболее вероятно, что оно будет находиться в диапазоне от -3 до +3. В этом можно убедиться, нажав клавишу F5 для повторного вычисления функции.
2. Постройте график гауссовой последовательности.
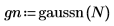
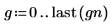
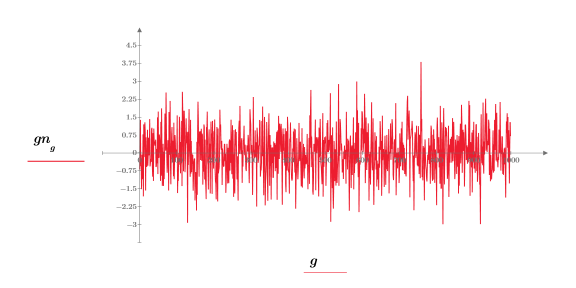
3. Подготовьте гауссовы данные для построения колоколообразной гистограммы, сгруппировав значения по 20 столбцам шириной 0.05.
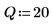
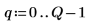
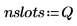
4. Определите вектор, который содержит граничные значения столбцов, и затем задайте самую правую границу.
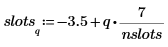
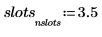
5. Используйте функцию hist, чтобы создать гистограмму, а затем постройте ее график в виде столбчатой диаграммы.
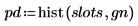
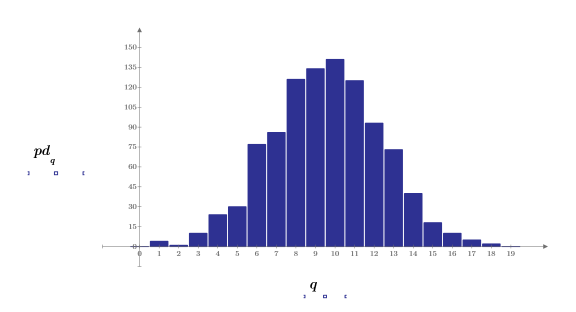
6. Сравните среднее значение и среднеквадратическое отклонение выборки с ожидаемыми значениями 0 и 1.
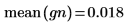
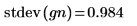
1/f-шум
Функция onefn вычисляет аппроксимацию 1/f-шума с использованием программы на основе алгоритма, разработанного Ричардом Воссом (см. колонку Мартина Гарднера в апрельском номере журнала Scientific American за апрель 1978 г.).
1. Используйте функцию onefn, чтобы создать вектор 1/f из 1000 точек.
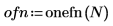
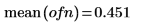
2. Путем настройки добейтесь среднего значения, равного 0.
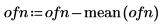
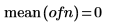
3. Постройте график данных вектора.
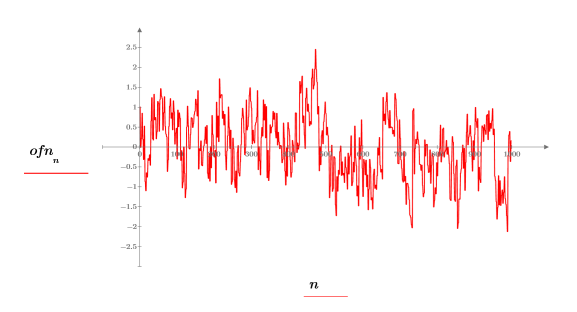
1/f-шум наблюдается во многих сигналах природного и искусственного происхождения, включая музыку, сигналы в мозге, погоду, флуктуации фондовых рынков и другие иерархически взаимодействующие системы. Например, при оцифровке образцов музыки различных стилей (рок, джаз, классическая) можно увидеть, что их спектры мощности очень близки по распределению к 1/f-шуму.
4. Используйте функцию lcorr, чтобы сравнить статистическую структуру такого шума со сгенерированным выше белым шумом путем вычисления автокорреляций.
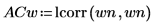
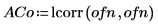
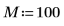
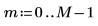
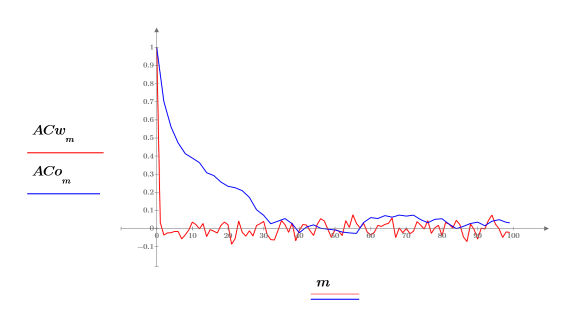
В отличие от белого шума, шум, создаваемый функцией onefn, является коррелированным, при этом корреляция затухает по мере увеличения запаздывания.
Сравнение шумовых сигналов с помощью спектров мощности
Другой способ анализа различий между белым шумом и 1/f-шумом заключается в сравнении спектров мощности.
1. Подготовьте 50 столбцов для 20 групп частот.
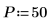
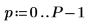
2. Используйте функции mag и dft для вычисления квадрата амплитуды частотного спектра для каждого сигнала.
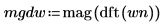
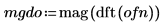
3. Выполните сглаживание результата путем усреднения по группам частот.
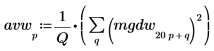
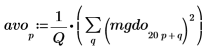
4. Постройте график спектра белого шума.
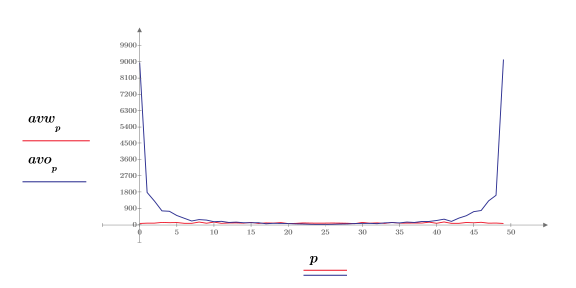
Как и ожидалось, спектр белого шума является фактически плоским. Спектр абсолютного значения аппроксимации 1/f-шума с увеличением частоты резко падает.
5. Используйте функцию log, чтобы вычислить более информативный логарифм амплитуды.
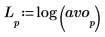
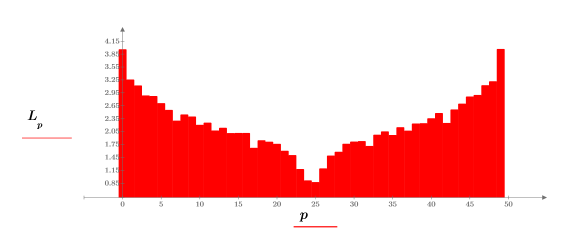
Эксперимент
В качестве эксперимента попытаемся создать спектр мощности 1/f-шума со случайными фазами, а затем выполнить обратное преобразование для получения вектора шума.
1. Задайте ширину спектра.
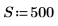
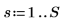
2. Используйте функцию exp для построения первой половины преобразования. Спектр мощности 1/f-шума соответствует спектру абсолютного значения 1/sqrt(f).
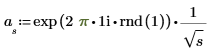
3. Вычислите вторую половину преобразования. (Для действительного сигнала вторая половина сопряженно-симметрична относительно средней точки.)
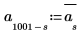
4. Задайте среднее значение шума равным нулю.
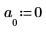
5. Используйте функцию idft для выполнения обратного преобразования Фурье (преобразование во временную область).
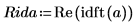
6. Постройте график вещественных значений обратного преобразования.
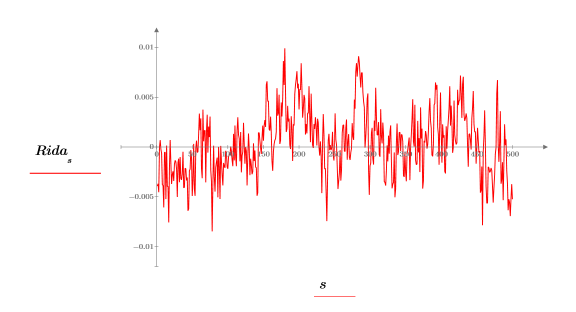
7. Используйте функцию lcorr для вычисления кривой автокорреляции.
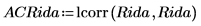
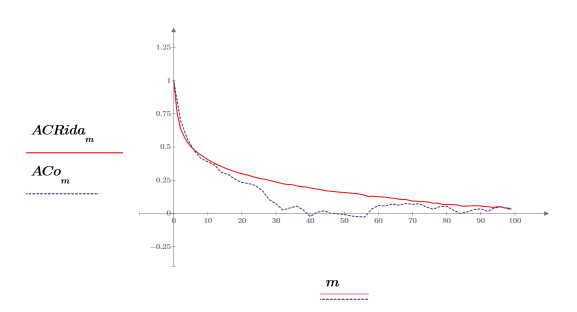
Поведение автокорреляции подобно выходным данным функции onefnс корреляцией 1.0 в точке 0 и различными степенями корреляции в других точках.