Экспоненциальные и логарифмические функции
• Функция exp(z) — возвращает число e, возведенное в степень z.
• Функция log(z, [b]) — возвращает основание b логарифма z. Если параметр b не указан, возвращает логарифм по основанию 10 числа z.
• Функция ln(z) — возвращает натуральный логарифм (по основанию e) числа z.
• ln0(z) - возвращает натуральный логарифм (по основанию e) числа z, но возвращает –1×10307 при z = 0.
Аргументы
• z — безразмерное скалярное значение (вещественное, комплексное или мнимое) или вектор скалярных значений.
Для функций log и ln значение z не может быть нулем. Если z - вектор, то ни один из его элементов не может быть нулем.
• b (необязательный) - положительный действительный скаляр или вектор скаляров. Если параметр b не указан, предполагается, что он равен 10.
Если b - вектор, то ни один из его элементов не может быть нулем и его длина должна совпадать с длиной вектора z.
|
|
• Для комплексных переменных z функции log возвращают значения из главной ветви этих функций, т. е. ln(z) = ln(|z|) + i arg(z)
• Функция exp эквивалентна возведению e в степень, но обе эти функции используют алгоритмы, отличные от стандартного возведения в степень. Для очень больших или очень малых значений показателя степени этот алгоритм более надежный, позволяющий избегать ошибок округления чисел. Наиболее точные значения для очень больших аргументов могут быть найдены с помощью аналитического преобразования функции exp(x) с десятичным аргументом: 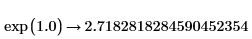 |