Дискретное преобразование Фурье для данных
• Функции dft(A), idft(Z) - возвращают прямое или обратное преобразование Фурье для вектора или матрицы, состоящих из комплексных значений.
Если вывод dft являются вектором V длины r, то:
◦ Вывод dft(V) - это вектор Z, имеющий длину r.
◦ Вывод idft(Z) - это вектор, имеющий длину r.
Если ввод dft - это матрица M с числом строк r и числом столбцов c, то:
◦ Вывод dft(M) - это матрица P с числом строк r и числом столбцов c.
◦ Вывод idft(P) является матрицей из r строк и c столбцов.
• dftr(B), idftr(Z) - возвращают прямое или обратное преобразование Фурье для вектора или матрицы, состоящих из вещественных значений.
Если вывод dftr являются вектором V длины r, то:
◦ Вывод dftr(V) представляет собой вектор Z длины L, где L=floor(r/2)+1. Элементы Z идентичны первым L элементам выходного параметра функции dft(V).
◦ Вывод idftr(Z) является вектором длины r=2(L-1).
Если ввод для dftr - это матрица M с числом строк r и числом столбцов c, то:
◦ Вывод dftr(M) является матрицей P с r строками и L столбцами, где L=floor(c/2)+1. Элементы P идентичны первым L столбцам выходного параметра функции dft(M).
◦ Вывод idftr(P) является матрицей из r строк и c=2(L-1) столбцов.
Аргументы
• A - вектор или матрица любого размера с комплексными значениями
• B — вектор или матрица действительных значений. Любая мнимая часть игнорируется. Если B - это вектор, число строк должно быть кратным 2. Если B - это матрица, число столбцов должно быть кратным 2.
• Единицы измерения данных для A и B должны быть совместимыми
Преобразование Фурье для векторов
• Если A - вектор, имеющий размерность m, то u-й элемент одномерного (1D) прямого преобразования вектора A определяется как Zu следующим образом:
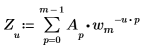
Где:
◦ m - число строк, а u определяется как: 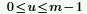
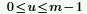
◦ i - мнимая единица, а wm определяется как:
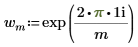
Вычисление Z в определенном выше определении эквивалентно применению функции dft к вектору A.
• Если Z - вектор, имеющий размерность m, то u-й элемент одномерного (1D) обратного преобразования вектора Z определяется как Au следующим образом:
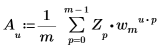
Где:
◦ Переменные m, u и wm определены выше.
Вычисление A в определенном выше определении эквивалентно применению функции idft к вектору Z.
Преобразование Фурье для матриц
• Если A - матрица, имеющая размерность mxn, то (u,v)-й элемент двумерного (2D) прямого преобразования матрицы A определяется как Zu,v следующим образом:
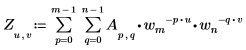
Где:
◦ Переменные m, u и wm определены выше.
◦ n - число столбцов, а v определяется как: 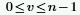
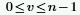
◦ i - мнимая единица, а wn определяется как:
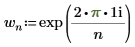
Вычисление Z в определенном выше определении эквивалентно применению функции dft к матрице A.
• Если Z - матрица, имеющая размерность mxn, то (u,v)-й элемент двумерного (2D) обратного преобразования матрицы A определяется как Au,v следующим образом:
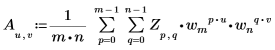
Где:
◦ Переменные m, n, u, v, wm и wn определены выше.
Вычисление A в определенном выше определении эквивалентно применению функции idft к матрице Z.
Дополнительная информация
• Функции преобразования Фурье выполняются быстрее, если число строк векторов и число столбцов в случае матриц является степенью числа 2.
• Новые функции dft/idft заменяют функциональность устаревших функций cfft/icfft и CFFT/ICFFT и значительно повышают производительность, особенно для наборов больших данных и в случаях, когда размер не является степенью числа 2.
• Новые функции dftr/idftr заменяют функциональность устаревших функций fft/ifft и FFT/IFFT.
Функция dftr оперирует с вещественными векторами, длина которых является четным числом, либо с матрицами, имеющими четное число столбцов.
• Функции fft/FFT оперируют только с вещественными векторами, длина которых является степенью числа 2.
• Выходные параметры функций ifft/IFFT имеют длину, равную только половине длины входного вектора плюс 1, или 2k-1+ 1, где k - целое число > 1. Оставшаяся половина, являющаяся сопряжением первой части с обратным порядком чисел, должна быть преобразована вручную. Функции dft/idft возвращают результат полной длины.
• Функции dft/idft отличаются от устаревших функций fft/ifft, FFT/IFFT и cfft/icfft, CFFT/ICFFT как коэффициентом масштабирования, так и знаком показателя степени.
◦ Различия для прямого преобразования
dft/dftr | fft/cfft | FFT/CFFT | |
|---|---|---|---|
Коэффициент масштабирования | 1 | 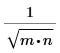 | 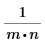 |
Знак показателя степени | Отрицательный | Положительный | Отрицательный |
◦ Различия для обратного преобразования
idft/idftr | ifft/icfft | IFFT/ICFFT | |
|---|---|---|---|
Коэффициент масштабирования | 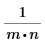 | 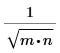 | 1 |
Знак показателя степени | Положительный | Отрицательный | Положительный |
При вычислении коэффициента масштабирования для функций, работающих только с векторами (случаи 1D), следует принимать n=1.