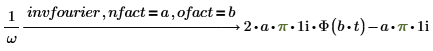Beispiel: Symbolische Transformationen
Führen Sie symbolische Fourier-, Laplace- und z-Transformationen und ihre Umkehrfunktionen durch.
Fourier- und inverse Fourier-Transformationen
1. Verwenden Sie das Schlüsselwort fourier, um die Fourier-Transformation der Dirac-Delta-Funktion Δ zu ermitteln.
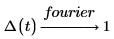
Erwartungsgemäß gibt diese Auswertung eine konstante Frequenz zurück.
2. Ermitteln Sie die Fourier-Transformation einer Funktion unter Beteiligung der Heaviside-Sprungfunktion Φ.
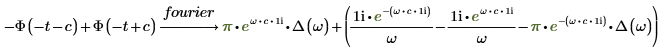
3. Fügen Sie zur Vereinfachung des Ergebnisses das Schlüsselwort simplify hinzu.
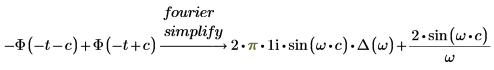
Z- und inverse Z-Transformationen
1. Verwenden Sie das Schlüsselwort ztrans, um die Z-Transformation der beiden folgenden Funktionen zu berechnen:
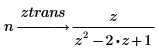
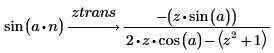
2. Verwenden Sie das Schlüsselwort invztrans, um die inverse Z-Transformation der beiden folgenden Funktionen zu berechnen:
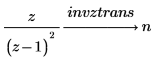
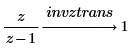
Standardvariable für eine Transformation ändern
1. Ermitteln Sie die inverse Laplace-Transformation einer Funktion.
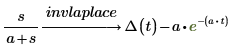
2. Ändern Sie in der Funktion, die durch die inverse Laplace-Transformation zurückgegeben wird, die Standardvariable t durch Hinzufügen eines Argumentenpaares nach dem Schlüsselwort "transform".
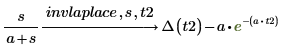
◦ Das erste Argument, s, ist die unabhängige Variable für die Definitionsbereichsfunktion.
◦ Das zweite Argument, t2, ist die neue unabhängige Variable für die transformierte Funktion.
◦ Die zurückgegebene inverse Laplace-Transformation verwendet die Variable t2 als unabhängige Variable. Δ ist die Dirac-Delta-Funktion.
◦ Sie können Δ zwar nicht mit dem numerischen Gleichheitszeichen, wohl aber mit dem symbolischen Auswertungsoperator auswerten.
3. Ermitteln Sie die Laplace-Transformation des Ergebnisses mit dem Schlüsselwort laplace.
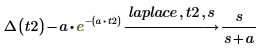
Mehr als ein Schlüsselwort zurzeit verwenden
Wenn die Ergebnisse einer symbolischen Berechnung nicht im gewünschten Format zurückgegeben werden, können Sie ein Schlüsselwort nach dem Schlüsselwort "transform" hinzufügen, um das Ergebnisformat zu ändern.
1. Ermitteln Sie die Z-Transformation einer Funktion.
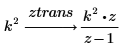
2. Verwenden Sie das Schlüsselwort expand zum Erweitern des Ergebnisses.
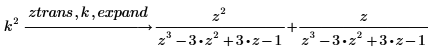
3. Verwenden Sie das Schlüsselwort laplace, um die Laplace-Transformation einer Funktion zu ermitteln.
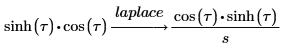
4. Verwenden Sie das Schlüsselwort simplify, um das Ergebnis in einem vereinfachten Format zu erhalten.
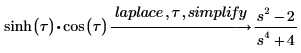
5. Ermitteln Sie die inversen Fourier-Transformationen der Funktionen sin und sinc, und stellen Sie die Ergebnisse in vereinfachter Form dar.
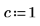
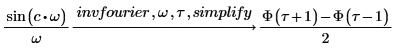
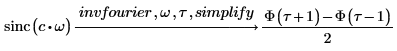
Verwenden Sie für Eingabefunktionen ohne symbolische Transformation die numerische Funktion dft.
Fourier-Transformation-Faktorisierung
1. Fügen Sie nfact und ofact zusammen mit fourier zu dem Ausdruck hinzu.
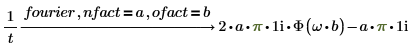
2. Fügen Sie nfact und ofact zusammen mit invfourier zu dem Ausdruck hinzu.