Diskrete Fourier-Transformation von Daten
• dft(A), idft(Z) – Gibt die Vorwärts- bzw. inverse Fourier-Transformation für einen komplexwertigen Vektor oder eine Matrix zurück.
Wenn die Eingabe für dft ein Vektor V der Länge r ist, dann gilt:
◦ Die Ausgabe von dft(V) ist ein Vektor Z der Länge r.
◦ Die Ausgabe von idft(Z) ist ein Vektor der Länge r.
Wenn die Eingabe für dft eine Matrix M mit r Zeilen und c Spalten ist, dann gilt:
◦ Die Ausgabe von dft(M) ist eine Matrix P von r Zeilen und c Spalten.
◦ Die Ausgabe von idft(P) ist eine Matrix von r Zeilen und c Spalten.
• dftr(B), idftr(Z) – Gibt die Vorwärts- bzw. inverse Fourier-Transformation für einen reellwertigen Vektor oder eine Matrix zurück.
Wenn die Eingabe für dftr ein Vektor V der Länge r ist, dann gilt:
◦ Die Ausgabe von dftr(V) ist ein Vektor Z der Länge L, wobei L=floor(r/2)+1. Die Elemente von Z sind identisch mit den ersten L Elementen der Ausgabe von dft(V).
◦ Die Ausgabe von idftr(Z) ist ein Vektor der Länge r=2(L-1).
Wenn die Eingabe für dftr eine Matrix M mit r Zeilen und c Spalten ist, dann gilt:
◦ Die Ausgabe von dftr(M) ist eine Matrix P mit r Zeilen und L Spalten, wobei L=floor(c/2)+1. Die Elemente von P sind identisch mit den ersten L Spalten der Ausgabe von dft(M).
◦ Die Ausgabe von idftr(P) ist eine Matrix von r Zeilen und c=2(L-1) Spalten.
Argumente
• A ist ein komplexwertiger Vektor oder eine Matrix beliebiger Größe.
• B ist ein reellwertiger Vektor oder eine entsprechende Matrix. Imaginärteile werden ignoriert. Ist B ein Vektor, so muss die Anzahl der Zeilen ein Mehrfaches von 2 sein. Ist B eine Matrix, so muss die Anzahl der Spalten ein Mehrfaches von 2 sein.
• Sowohl für A als auch für B müssen die Daten kompatible Einheiten aufweisen.
Fourier-Transformation von Vektoren
• Wenn A ein Vektor der Größe m ist, wird das u-te Element der eindimensionalen Vorwärtstransformation von Vektor A durch Zu folgendermaßen angegeben:
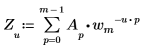
Dabei gilt:
◦ m ist die Anzahl von Zeilen, und u ist definiert als: 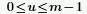
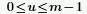
◦ i ist die imaginäre Einheit, und wm ist definiert als:
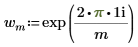
Die Auswertung von Z in der obigen Definition entspricht der Anwendung der Funktion dft auf den Vektor A.
• Wenn Z ein Vektor der Größe m ist, wird das u-te Element der eindimensionalen inversen Transformation von Vektor Z durch Au folgendermaßen angegeben:
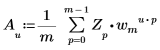
Dabei gilt:
◦ m, u und wm werden oben definiert.
Die Auswertung von A in der obigen Definition entspricht der Anwendung der Funktion idft auf den Vektor Z.
Fourier-Transformation von Matrizen
• Wenn A eine Matrix der Größe mxn ist, wird das (u,v)-te Element der zweidimensionalen Vorwärtstransformation von Matrix A durch Zu,v folgendermaßen angegeben:
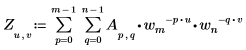
Dabei gilt:
◦ m, u und wm werden oben definiert.
◦ n ist die Anzahl von Spalten, und v ist definiert als: 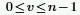
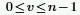
◦ i ist die imaginäre Einheit, und wn ist definiert als:

Die Auswertung von Z in der obigen Definition entspricht der Anwendung der Funktion dft auf die Matrix A.
• Wenn Z eine Matrix der Größe mxn ist, wird das (u,v)-te Element der zweidimensionalen inversen Transformation von Matrix A durch Au,v folgendermaßen angegeben:
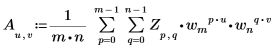
Dabei gilt:
◦ m, n, u, v, wm und wn werden oben definiert.
Die Auswertung von A in der obigen Definition entspricht der Anwendung der Funktion idft auf die Matrix Z.
Zusätzliche Informationen
• Fourier-Funktionen werden schneller ausgeführt, wenn die Anzahl der Vektorzeilen und Matrixspalten eine Potenz von 2 ist.
• Die neuen dft/idft Funktionen ersetzen die Funktionalität der veralteten Funktionen cfft/icfft und CFFT/ICFFT und bieten eine wesentliche Leistungsverbesserung, insbesondere bei größeren Datensätzen und in Fällen, in denen die Größe eine Potenz von 2 ist.
• Die neuen dftr/idftr Funktionen ersetzen die Funktionalität der veralteten Funktionen fft/ifft und FFT/IFFT.
Die Funktion dftr verarbeitet reelle Vektoren, deren Länge eine gerade Zahl ist, sowie Matrizen mit einer geraden Anzahl von Spalten.
• fft/FFT-Funktionen verarbeiten reelle Vektoren, deren Länge eine Potenz von 2 ist.
• ifft/IFFT-Funktionen haben nur die Hälfte der Länge des Eingabevektors plus eins oder 2k-1+1, wobei k eine Ganzzahl > 1 ist. Die andere Hälfte, der konjugierte Teil des ersten Teils mit umgekehrter Reihenfolge, muss manuell rekonstruiert werden. Die Funktionendft/idft übergeben das vollständige Ergebnis.
• Die Funktionen dft/idft unterscheiden sich von den abgelehnten Funktionen fft/ifft, FFT/IFFT und cfft/icfft, CFFT/ICFFT sowohl hinsichtlich des Skalierungsfaktors als auch in Bezug auf das Exponentenvorzeichen.
◦ Bei den Vorwärtstransformationen gibt es folgende Unterschiede:
dft/dftr | fft/cfft | FFT/CFFT | |
|---|---|---|---|
Skalierungsfaktor | 1 | 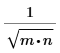 | 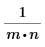 |
Exponentenvorzeichen | Negativ | Positiv | Negativ |
◦ Bei den inversen Transformationen gibt es folgende Unterschiede:
idft/idftr | ifft/icfft | IFFT/ICFFT | |
|---|---|---|---|
Skalierungsfaktor | 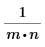 | 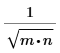 | 1 |
Exponentenvorzeichen | Positiv | Negativ | Positiv |
Gehen Sie bei der Berechnung des Skalierungsfaktors für Funktionen, die nur Vektoren bearbeiten (eindimensionale Fälle), davon aus, dass n=1 ist.