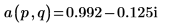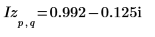Beispiel: dft und idft einer Matrix
Verwenden Sie die Funktionen dft und idft, um die vorwärtsgerichtete oder inverse diskrete Fourier-Transformation einer Matrix zu suchen.
1. Legen Sie die Dimensionen einer Datenmatrix fest.
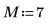
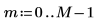
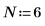
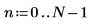
2. Verwenden Sie die Funktion exp, um eine komplexe Datenmatrix mit den Dimensionen MxN zu erstellen.
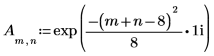
3. Verwenden Sie die Funktion dft, um die diskrete Fourier-Transformation von A zu berechnen.
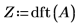
4. Verwenden Sie die Definition von dft, um ein bestimmtes Element von Z zu berechnen.
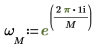
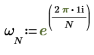
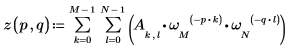
5. Verwenden Sie die oben genannte Definition, um ein bestimmtes Frequenzelement zu suchen und mit der Ausgabe der Funktion dft zu vergleichen.
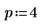
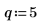
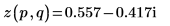
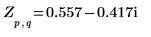
Gaußsche idft
Die Funktion idft ist die inverse Transformation von dft. Sie akzeptiert eine reelle oder komplexe Matrix als Argument und gibt eine Matrix mit den gleichen Dimensionen zurück.
1. Zeigen Sie, dass die inverse Transformation einer dft-Funktion die Funktion selbst ist.
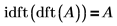
2. Verwenden Sie die zuvor definierte Matrix A, und zeigen Sie dann, dass die inverse Transformation einer Funktion dft die Funktion selbst ist.
 |  |
3. Verwenden Sie die Definition von idft, um jedes Element von A zu berechnen.
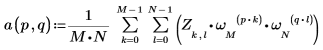
4. Verwenden Sie die oben genannte Definition, um ein bestimmtes Frequenzelement zu suchen und mit dem entsprechenden Element in der Ausgabe der Funktion idft zu vergleichen.