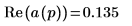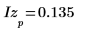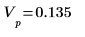Beispiel: dft und idft eines Vektors
Verwenden Sie die Funktionen dft und idft, um die vorwärtsgerichtete oder inverse diskrete Fourier-Transformation eines Vektors zu suchen.
1. Legen Sie die Länge eines Datenvektors fest.
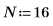
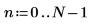
2. Erstellen Sie mit der Funktion exp einen reellen Datenvektor der Länge N.
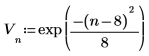
3. Plotten Sie die Daten.
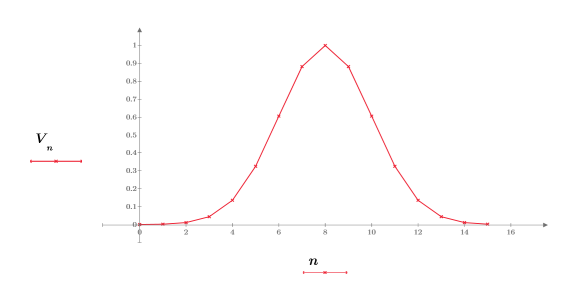
4. Verwenden Sie die Funktion dft, um die diskrete Fourier-Transformation von V zu berechnen.
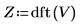
5. Stellen Sie die absoluten Werte von Z grafisch dar.
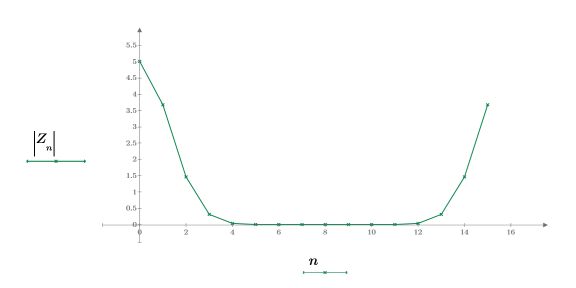
6. Zeigen Sie die Definition der Funktion dft an.
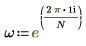
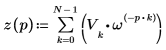
7. Verwenden Sie die obengenannte Definition, um ein bestimmtes Frequenzelement zu suchen und mit dem entsprechenden Element in der Ausgabe der Funktion dft zu vergleichen.
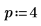
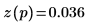
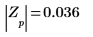
Gaußsche idft
Die Funktion idft ist die inverse Transformation von dft. Sie akzeptiert einen reellen oder komplexen Vektor als Argument und gibt einen Vektor der gleichen Länge zurück.
1. Zeigen Sie, dass die inverse Transformation einer Funktion dft die Funktion selbst ist.
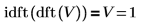
2. Nehmen Sie den zuvor definierten Vektor V, und zeigen Sie, dass die inverse Funktion dft von V gleich V ist.
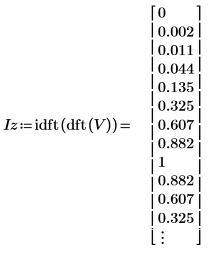 |  |
3. Zeigen Sie die Definition der Funktion idft an.
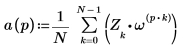
4. Verwenden Sie die obengenannte Definition, um ein bestimmtes Frequenzelement zu suchen und mit dem entsprechenden Element in der Ausgabe der Funktion idftund dem Vektor V zu vergleichen.