Exponential- und Logarithmusfunktionen
• exp(z) – Gibt die Zahl e hoch z zurück.
• log(z, [b]) – Gibt den Logarithmus von z zur Basis b zurück. Wenn b weggelassen wird, gibt es den Logarithmus von z zur Basis 10 zurück.
• ln(z) – Gibt den natürlichen Logarithmus (Basis e) von z zurück.
• ln0(z) – Gibt den natürlichen Logarithmus (Basis e) von z zurück, gibt jedoch –1×10307 bei z = 0 zurück.
Argumente
• z ist ein dimensionsloser Skalar (reell, komplex oder imaginär) oder ein Vektor aus Skalaren.
Für die Funktionen log und ln kann z nicht null sein. Wenn z ein Vektor ist, kann keines seiner Elemente eine Null sein.
• b (optional) ist ein positiver reeller Skalar- oder Skalarvektor. Wird b weggelassen, wird ein Wert von 10 angenommen.
Wenn b ein Vektor ist, kann keines seiner Elemente eine Null sein, und er muss dieselbe Länge wie Vektor z haben.
|
|
• Bei komplexem z geben die log-Funktionen Werte aus dem Hauptzweig dieser Funktionen oder ln(z) = ln(|z|) + i arg(z) zurück.
• Die Funktion exp entspricht der Potenzierung von e, beide verwenden jedoch einen anderen Algorithmus als die standardmäßige Potenzierung. Für sehr große oder kleine Werte im Exponenten ist dieser Algorithmus robuster, was das Vermeiden von numerischen Rundungsfehlern angeht. Die genauesten Werte für sehr große Argumente können mit der symbolischen Auswertung von exp(x) mit einem dezimalen Argument gefunden werden: 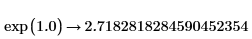 |