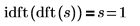Beispiel: DFT von komplexen Funktionen
Verwenden Sie die Funktionen dft und idft, um die komplexe oder reelle Fourier-Transformation bzw. die inverse Fourier-Transformation zu berechnen.
1. Erstellen Sie einige simulierte komplexe Daten mit N Datenpunkten.
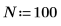
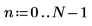
2. Definieren Sie den Stichprobenabstand.
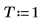
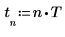
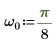
3. Verwenden Sie die Funktion exp, um das folgende Signal zu definieren.
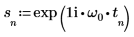
4. Definieren Sie die Abtastfrequenz und die Frequenz, die dem n-ten Eintrag im transformierten Vektor entspricht.
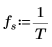
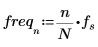
5. Wenden Sie die Funktion dft an, um die Daten in den Frequenzbereich zu transformieren.
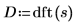
6. Speichern Sie den Betrag der Elemente von Array D in einem neuen Array.
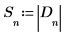
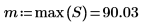
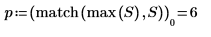
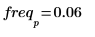
8. Stellen Sie den Betrag von DFT als Frequenzfunktion dar.
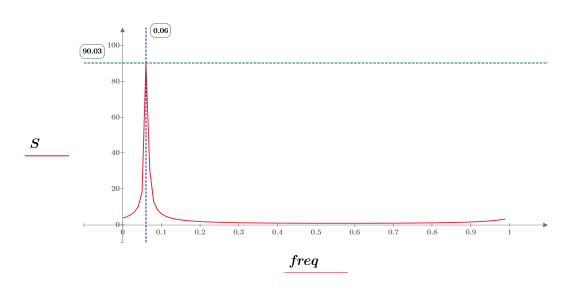
9. Zeigen Sie, dass die Frequenz des Spitzenwerts ω0/2π entspricht.
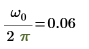
10. Zeigen Sie unter Verwendung der Funktion idft, dass die IDFT einer DFT eines Signals das Signal selbst liefert.