ODE 풀이 함수
• 아래의 각 함수는 (intvls+1)×(n+1) 해 행렬을 구합니다. 여기서, n은 미지수의 수입니다. 행렬의 첫 번째 열에는 해가 계산되는 x 값이 포함됩니다. 이러한 값은 x1과 x2 사이에서 (intvls + 1)로 일정한 간격을 이루는 숫자입니다. 나머지 열에는 첫 번째 열의 x 값에 해당하는 해(y0,y1,...,yn-1)의 값이 들어 있습니다.
• rkfixed, RkAdapt, Bulstoer, Stiffb 및 Stiffr 풀이 함수의 경우 해당 풀이 함수를 호출하기 전에 변수 TOL을 정의하여 해에 대한 스칼라 공차를 지정할 수 있습니다. 예를 들어, 모든 변수에 대한 공차를 10-6으로 설정할 수 있습니다.
TOL:=10-6
TOL은 풀이 함수 Adams, BDF 또는 Radau에 대한 공차에 영향을 주지 않습니다. 이러한 풀이 함수의 경우 선택적 인수인 tol을 사용하여 공차를 지정해야 합니다.
• ODE 풀이 구간을 사용하여 방정식 및 초기 조건 항목을 단순화할 수 있습니다.
가파르지 않은 시스템 풀이
• Adams(init, x1, x2, intvls, D, [tol]) - Adams 방법을 사용합니다.
• rkfixed(init, x1, x2, intvls, D) - 4차 Runge-Kutta 고정 단계 방법을 사용합니다.
• Rkadapt(init, x1, x2, intvls, D) - 적응 단계 크기를 사용하는 4차 Runge-Kutta 방법을 사용합니다.
• Bulstoer(init, x1, x2, intvls, D) - Runge-Kutta 방법보다 약간 더 정확하지만 변화가 완만한 시스템이 필요한 Bulirsch-Stoer 방법을 사용합니다.
가파른 시스템 풀이
이러한 함수를 사용하여 가파른 또는 대수 ODE 문제를 풉니다.
• BDF(init, x1, x2, intvls, D, [J], [tol]) - 역 미분 수식 방법을 사용합니다. 선택적 인수인 J 또는 tol을 사용하거나 다른 인수를 생략할 수 있습니다.
• Radau(init, x1, x2, intvls, D, [J], [M], [tol]) - Radau5 방법을 사용합니다. 선택적 인수인 J, M 및 tol의 임의 조합을 사용하고 사용하지 않을 옵션은 생략할 수 있습니다.
• Stiffb(init, x1, x2, intvls, D, AJ) - Bulirsch-Stoer 방법을 사용합니다.
• Stiffr(init, x1, x2, intvls, D, AJ) - Rosenbrock 방법을 사용합니다.
혼성 풀이 함수
• AdamsBDF(init, x1, x2, intvls, D, [J], [tol]) - 시스템이 가파른지 여부를 확인하고 그에 따라 Adams 또는 BDF를 호출합니다. 선택적 인수인 J 또는 tol을 사용하거나 다른 인수를 생략할 수 있습니다.
인수
• init는 n개의 실수 초기치로 이루어진 벡터이거나 단일 스칼라 초기치(단일 ODE인 경우)입니다. 여기서 n은 미지수의 수입니다.
• x1 및 x2는 ODE 해를 계산하는 구간의 스칼라 끝점(실수)입니다. init의 초기치는 x1에서 계산된 ODE 함수의 값입니다.
• intvls는 풀이 함수를 보간하는 데 사용되는 이산화 간격의 수(정수)입니다. 해 점의 수는 intervals + 1입니다.
• D는 시스템의 우변을 지정하는 D(x,y) 형식의 벡터 함수입니다.
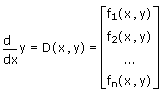
• tol(선택 사항)은 시스템의 독립 변수 각각에 대한 공차를 지정하는 실수 값 또는 실수 값의 벡터입니다. 공차는 해 변수에 필요한 정확도입니다.
◦ tol을 10-5보다 작거나 같은 값으로 설정해야 합니다. 문제의 배율 및 사용된 상대 단계 크기에 따라, 적합한 해를 구하기 위해 TOL 값을 줄여야 할 수 있습니다. tol의 값이 작을수록 풀이 알고리즘에서 필요한 정확도를 얻기 위해 수행할 단계가 많아집니다.
◦ 방정식 시스템을 풀고 있는 경우 tol을 스칼라 값으로 설정하면 시스템의 모든 변수에 대해 동일한 공차가 지정됩니다. tol을 벡터(길이가 시스템의 변수 개수와 동일한 벡터)로 설정하면 각 변수에 대해 개별 공차가 지정됩니다.
• J(선택 사항)는 야코비 행렬을 반환하는 J(x, y) 형식의 함수입니다. 여기서 야코비 행렬은 y0,y1,...yn−1을 기준으로 하는 D 함수의 편도함수 행렬입니다.
• M(선택 사항)은 M · dy/dt = f(t, y) 형식의 변수 간 연결을 나타내는 실수 행렬입니다.
• AJ는 첨가된 야코비를 반환하는 AJ(x, y) 형식의 함수입니다. 이 첨가된 야코비 행렬의 첫 번째 열에는 시스템의 우변에 있는 x 기준 함수의 편도함수가 포함됩니다. 나머지 열은 y0,y1,...yn−1 기준의 편도함수가 포함된 야코비 J 열입니다.
D, J 및 AJ 함수는 인수 없이 풀이 함수에 제공되고, yn(x) 함수는 인수 없이 D, J 및 AJ에 지정됩니다.
D, J 및 AJ에 대한 두 번째 인수는 항목이 하나뿐인 경우에도 벡터 아래 첨자로 표시됩니다.
추가 정보
• Radau 및 Rkadapt 함수에서는 미분 방정식을 풀 때 균일하지 않은 단계 크기를 내부적으로 사용하며 해의 변화가 큰 영역에서는 단계를 더 많이 추가하지만 intvls에 지정된 개수의 간격이 일정한 점에서 해를 구합니다.
• Radau를 사용할 경우 야코비 입력이 필요 없다는 장점이 있지만 J를 즉시 사용할 수 있는 경우에도 이 방법을 사용하면 정확도가 향상됩니다.