ODE 초기 조건 구하기
다음 함수는 초기 조건 일부가 알려지지 않은 경계값 문제에 사용됩니다.
• bvalfit(v1, v2, x1, x2, xf, D, load1, load2, scoreb)
• sbval(v1, x1, x2, D, load1, scorei)
D로 지정되는 ODE 또는 ODE 시스템에서 x1에 대해 정의되어 있지 않은 초기치를 포함하는 벡터를 구합니다. 계산된 초기치는 ODE 풀이 중 하나에 사용할 수 있습니다. 해의 값 중 일부와 중간 값에서의 해당 1차 n − 1 도함수를 알고 있으면 bvalfit를 사용합니다. 이 함수는 적분 구간에서 도함수가 단절되어 있는 경우에 특히 유용합니다. 초기 점과 끝 점에서의 값 중 일부를 알고 있으면 sbval을 사용합니다. 경계값 문제를 끝점에서 평활하고 해의 궤적과 중간 점에서의 도함수를 일치시키면 초기치 문제로 변환됩니다.
인수
• v1, v2는 x1에 대해 정의되지 않은 초기치의 실수 추측값 벡터입니다.
• x1, x2는 미분 방정식의 해가 계산되는 구간의 실수 끝점입니다.
• xf는 해의 궤적이 동일해야 하는 x1과 x2 사이의 실수 중간 점입니다.
• D(x, y)는 독립 변수 x의 n요소 벡터 값 함수와 ODE 시스템 내 모든 미지 함수의 1차 도함수 방정식이 있는 y 함수 벡터입니다.
이 벡터를 생성하려면 승수와 고차 도함수 없이 좌변에 1차 도함수 항만 두고 방정식을 계산합니다. 예를 들어 2차 도함수가 포함된 y(x) 함수의 단일 ODE는 y0(x) 및 y1(x)(여기서 y0의 1차 도함수는 y1)의 방정식 시스템으로 작성되어야 합니다. 단일 함수 ODE는 풀이 함수에 맞게 다시 작성되며, 이때 벡터 아래 첨자를 아래와 같이 사용합니다.
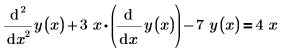
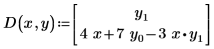 | 암시적 좌변 사용 | 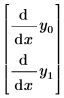 |
• load1(x1, v1), load2(x2, v2)는 요소가 각각 x1 및 x2에 대한 yn 값에 해당하는 벡터 값 함수입니다. 이 함수 값 중 일부는 알려진 초기 조건입니다. 미지 값은 각각 v1과 v2에서 구한 해당 추측값으로 설정됩니다.
• scoreb(xf, y)는 xf에서 해를 일치시키는 방법을 지정하는 데 사용되는 실수 벡터 값 함수입니다. 일반적으로 scoreb(xf, y):= y를 정의하여 모든 미지 함수의 해가 xf에서 일치하도록 해야 합니다.
• scorei(x2, y)는 v와 요소 수가 같은 실수 벡터 값 함수입니다. 각 요소는 원래 정의된 x2에 대한 초기 조건과 풀이에서 추정된 해의 차이를 나타냅니다. score 벡터는 x2에 대해 추정된 해가 초기 조건에 얼마나 가까운지를 나타냅니다. 값이 0인 요소는 완벽하게 일치함을 나타냅니다.