미분 방정식 풀이 정보
상미분 방정식(ODE) 풀이 함수는 하나의 변수를 사용하는 미지 함수에 대한 방정식 또는 방정식 시스템을 풉니다. 편미분 방정식(PDE) 풀이 함수는 두 개의 변수를 사용하는 함수에 대한 방정식을 풉니다(1D PDE).
상미분 방정식
풀이 구간을 만들지 않고 직접 ODE를 풀이하려면 다음과 같은 형식의 ODE 시스템을 푸는 ODE 풀이 시스템 중 하나를 사용하십시오.
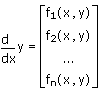
여기서 y는 독립 변수 x로 이루어진 미지 함수의 벡터입니다. 고차수 ODE를 풀이하려면 1차 ODE 시스템으로 다시 쓰십시오.
ODE 풀이 함수는 가파른 시스템 풀이와 가파르지 않은 시스템 풀이의 두 가지 형식으로 구분됩니다. y’=Ay처럼 행렬 형식으로 작성된 ODE 시스템에서 A가 근접 특이 행렬인 경우에는 가파른 시스템이라고 하며, 그렇지 않은 경우에는 가파르지 않은 시스템이라고 합니다.
• Adams - Adams-Bashford 방법입니다.
• rkfixed, Rkadapt, Bulstoer - 고정 및 적응 단계 크기를 사용하는 4차 Runge-Kutta 방법 및 변화가 완만한 ODE에 대한 Bulstoer 방법입니다.
• BDF - 역 미분 수식 방법입니다.
• Radau, Stiffb, Stiffr - 가파른 시스템에 사용하는 RADAU, Bulirsch-Stoer 및 Rosenbrock 방법입니다.
• statespace - 선형 1차 ODE 시스템입니다.
• bvalfit, sbval - 초기 조건 일부가 알려지지 않은 경우 선형 사격법에 의해 초기치 문제로 변환된 경계값 문제입니다.
특정 ODE 또는 일반적인 ODE를 푸는 특수 다항식 생성기 및 초기하 함수에도 여러 가지가 있습니다.
편미분 방정식
• numol - 연결된 ODE 및 대수 제약 조건을 포함하여 1D PDE의 쌍곡선 시스템 및 포물선 시스템에 대한 명령줄 풀이 함수입니다.
• relax, multigrid - 포아송(Poisson)/라플라스(Laplace) 타원 PDE에 대한 명령줄 풀이 함수입니다.
• numol은 과도 1D 쌍곡선 및 포물선 PDE(x,t의 함수)를 풀기 위한 것입니다.
• multigrid는 제곱에 대한 정상 상태 2D 타원 PDE(x,y의 함수)를 풀기 위한 것입니다.
야코비
• Jacob - 벡터의 야코비 행렬을 구합니다.