ODE 풀이
풀이 구간과 odesolve 함수를 사용하여 지정된 값 범위에 대해 상미분 방정식(ODE)을 충족하는 함수를 구할 수 있습니다.
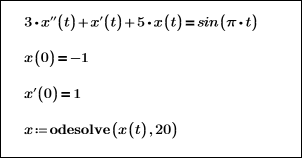
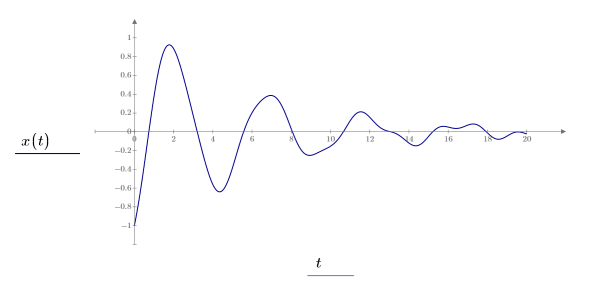
여기에서는 범위 0 ≤ x ≤ 20에 대해 출력 함수를 풉니다.
풀이 구간에서 ODE를 사용할 때 다음과 같은 제약 조건에 주의해야 합니다.
• 연산자 - ODE를 풀려면 풀이 구간에서 같음 연산자를 사용합니다. 비교 연산자나 부등호 연산자를 사용하지 마십시오. 도함수를 정의할 경우 d/dx 및 d2/dx2 또는 y'(x) 및 y''(x) 같은 도함수 또는 프라임 연산자를 사용합니다.
• 초기 및 경계 조건 - 단일 n차 ODE의 경우 n개의 독립된 등호 제약 조건이 있어야 합니다.
◦ 초기치 문제 - 단일 초기점 a에 y(x) 값과 해당 1차 n − 1 도함수가 필요합니다.
◦ 경계값 문제 - n 제약 조건은 초기점 y(x) 또는 끝점 a에서 b의 특정 값과 해당 도함수를 지정해야 합니다. 제약 조건은 sbval 함수에 대한 입력 요구사항을 충족해야 합니다. 경계값 조건을 제공할 때 odesolve 함수가 sbval을 호출합니다.
각각의 경우 경계 조건에서 사용하는 끝점은 odesolve 명령에서 지정한 끝점과 일치해야 합니다. PTC Mathcad에서는 올바른 형식 및 제약 조건 수를 검사하고 잘못 입력된 경우 오류를 반환합니다.
• 대수 제약 조건 - y(b) + z(b) = w(b) 같은 대수 제약 조건을 추가할 수 있습니다. 그러면 풀이 구간에 odesolve에서 출력 함수 중 하나로 지정해야 하는 추가 미지 함수 w가 포함됩니다.
• 출력 - odesolve의 출력을 인수가 없이 함수 이름이나 함수 이름의 벡터에 지정해야 합니다.
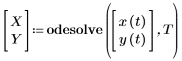
이러한 함수의 암시적 인수는 적분 변수입니다.
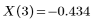

풀이 방법
• 문제의 배율 및 사용한 상대 단계 크기에 따라, 적합한 해를 구하기 위해 TOL 값을 줄여야 할 수 있습니다. PTC Mathcad odesolve에서 적분 단계가 너무 많다는 메시지가 나타나면 이 방법을 시도해 보십시오.
• 풀려는 함수가 적분 구간에서 특이점을 포함하지 않아야 합니다. 그렇지 않으면 불안정한 결과가 나타날 수 있습니다.
• 여러 주기에 걸친 주기적인 동작과 관련된 문제를 풀 때는 앨리어싱이 발생할 수 있습니다. 결과에서 예상한 도수를 얻으려면 보간 점의 수를 늘려야 합니다.
• 최고차 도함수 항에서 선형이 아닌 ODE를 풀이하거나 프로그램 루프에서 ODE를 풀이하려면 rkfixed 또는 다른 명령줄 ODE 풀이 시스템 중 하나를 사용하십시오. 매개변수화된 풀이 구간의 출력을 부분 변수 함수를 사용하여 프로그램 루프에서 지정할 수도 있습니다.