PDE의 완화법
• relax(A, B, C, D, E, S, U, rjac)
• multigrid(M, ncycle)
행렬에서 요소의 위치가 정사각형 영역에서 값의 위치에 해당하고 요소의 값이 해당 점에 대한 포아송(Poisson) 편미분 방정식PDE의 근사치인
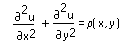
정방 행렬입니다. relax 함수는 격자선상의 SOR(Successive OverRelaxation)법으로 수정된 가우스-사이델(Gauss-Seidel) 기법을 사용하여 포아송 방정식을 풉니다.
multigrid 함수는 U의 모든 경계 조건이 0인 특수한 경우에 multigrid 방법을 사용하여 방정식을 풉니다.
• 경계 조건이 일정하고 4개 방향에서 동일한 경우 모든 방향에서 0개의 경계 조건을 갖도록 방정식을 변환하고 multigrid를 사용하면 더 빠르고 쉽게 설정할 수 있습니다.
• ρ = 0인 경우 포아송 방정식은 라플라스 방정식으로 바뀝니다.
• 쌍곡선 또는 포물선 PDE나 PDE의 시스템을 풀려면 numol을 사용하십시오.
인수
• A, B, C, D, E 는 가장 가까운 근방 데이터 점 4개와 근사 점에 대한 u 함수의 이산 라플라스(Laplace) 근사 계수를 포함하는 크기가 같은 실수 정방 행렬입니다.
• S는 정사각형 내의 각 점에 대한 소스 항이 포함된 정방 행렬입니다.
• U는 영역의 가장자리를 따라 있는 경계 값과 영역 내에 있는 해의 초기 추측값이 포함된 정방 행렬입니다.
• rjac는 0 < rjac < 1인 실수값으로, 야코비 반복법의 스펙트럼 반경을 나타냅니다. 이 값은 완화법 알고리즘의 수렴을 제어합니다.
rjac의 최적 값은 구체적인 문제에 따라 다르지만 r이 적절한 시작점이 될 수 있습니다. 여기서 n은 격자선의 각 방향에 있는 점의 수를 나타냅니다.
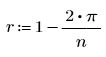
• M은 정사각형 영역의 점에 해당하는 소스 항을 나타내는 요소로 이루어진 1 + 2n 정방 행렬입니다.
• ncycle은 multigrid 반복법의 각 레벨에 대한 주기 수를 나타내는 정수입니다.
ncycle 값이 2이면 대개 해에 대한 적절한 근사값이 됩니다.