Modelos eulerianos y ecuaciones gobernantes
En esta sección se explican las ecuaciones gobernantes para los modelos de volumen de fluido (VOF) y multifase de mezcla, el modelado de la turbulencia y los límites en flujos multifase.
Ecuaciones gobernantes multifase generales
En el método Euler-Euler, se supone que las diferentes fases o componentes de un sistema multifase son matemáticamente continuos interpenetrantes y que comparten la misma presión de flujo. Puesto que el espacio físico o volumen se comparte entre todas las fases, se introduce el concepto de fracción volumétrica de fase para describir el transporte de fase. Se supone que las fracciones volumétricas de fase son funciones continuas de espacio y tiempo, y que su suma es igual a uno. Se aplican las leyes de la conservación para cada fase a fin de derivar un conjunto de ecuaciones gobernantes, que se cierran por relaciones constitutivas teóricas o empíricas. El método Euler-Euler tiene dos tipos de modelos que se utilizan habitualmente:
• Modelo de varios fluidos no homogéneos o euleriano: se resuelven directamente las ecuaciones gobernantes en cada fase, incluidas las ecuaciones de la fase de fracción de momento, energía, turbulencia, especies y volumen. Las interacciones fase-a-fase y las transferencias interfásicas de momento, masa, especies y calor se modelan mediante submodelos físicos.
Mediante la utilización de la fase escalar general, ϕq, q para la frase qth, la ecuación generalizada para la fase q tiene la siguiente forma:
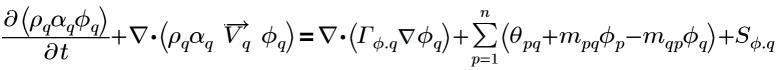
ecuación 2.54
donde,
ρq | densidad q |
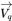 | Velocidad |
Sϕq | término de origen |
Tϕq | coeficiente de difusión |
αq | fracción de volumen de la fase qth |
y ϕq representa las variables dependientes en un sistema multifase:
ecuación 2.55
donde,
Uq, Vq, Wq | componentes de la velocidad de fase |
Hq | entalpía total de fase |
Yqi | fracción másica de la especie "i" en la fase qth |
k | energía cinética turbulenta |
ε | índice de disipación de energía cinética turbulenta para los modelos de k-ε |
En la ecuación 2.54, el segundo término a la derecha representa los intercambios interfase. En concreto,
p | fase pth |
n | número de fases del sistema multifase |
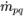 | transferencia de masa de la fase qth a la fase pth |
θpq | intercambio de fase directo de las cantidades de transporte, incluidos el momento, la energía y las especies |
Mediante la utilización de submodelos para intercambios interfase de especies, masa, momento y calor, se puede derivar el conjunto completo de ecuaciones gobernantes del flujo a partir de las ecuaciones de transporte que se generalizan aquí.
• Modelo multifase homogéneo: alternativa simplificada y económica al modelo no homogéneo. El método de modelado homogéneo permite calcular el promedio de las ecuaciones de flujo, energía y turbulencia gobernantes de la fase para obtener un conjunto de ecuaciones de transporte de la mezcla, mientras las fracciones volumétricas de la fase siguen resueltas. Para la mezcla escalar, ϕm, la expresión de la ecuación gobernante generalizada es la siguiente:
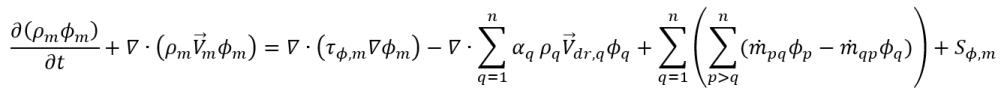
ecuación 2.56
donde,
m | mezcla de fases |
todas las variables con m | valores promedio de mezcla o fase |
y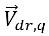 
es la diferencia entre la velocidad de la fase q y la velocidad de la mezcla:
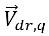es la diferencia entre la velocidad de la fase q y la velocidad de la mezcla: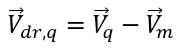
El modelo multifase homogéneo es un caso limitante del flujo multifase de Euler-Euler en el que la velocidad de transferencia interfase es grande. La suposición fundamental es que todas las fases comparten el mismo campo de presión. Con esta suposición, el modelo homogéneo simplifica más el modelo de varios fluidos euleriano no homogéneo completo si se supone que todas las fases comparten un campo común de velocidad, temperatura y turbulencia. Este método es un buen sustituto para el modelo euleriano de varios fluidos completo debido a su fácil implementación y economía computacional. Físicamente, sin el requisito de los modelos de intercambio interfase en las ecuaciones de momento y energía, el modelo homogéneo puede funcionar igual que el modelo de varios fluidos completo en casos como, por ejemplo, los flujos en superficie libre (VOF), la cavitación u otros flujos multifase altamente mezclados.
En Creo Flow Analysis, el módulo multifase actual solo adopta el método de modelado homogéneo. La atención se centra en el modelado de flujo en superficie libre (modelo de volumen de fluido) y los flujos de dos fases líquido-gas homogéneos (modelo de mezcla). En principio, se puede aplicar la capacidad de modelado para flujos de n fases.
Modelos multifase de VOF y mezcla
Los modelos multifase de volumen de fluido (VOF) y mezcla utilizan el método de modelado homogéneo. La ecuación de transporte de la fracción volumétrica en cada fase se obtiene de la ecuación 2.54. Las ecuaciones gobernantes para el momento y la energía de la mezcla se derivan mediante la ecuación 2.56 y las leyes de conservación de masa, momento y energía. En esta sección, se presenta el conjunto de ecuaciones gobernantes.
• Ecuación de fracción volumétrica de fase q
En la ecuación 2.54, si se define ϕq=1, se obtiene la ecuación de fracción volumétrica de la fase q:
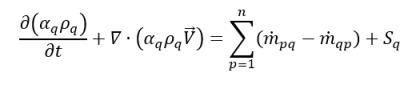
ecuación 2.57
donde los términos de intercambio de velocidad de masa,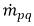 
y 
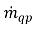representan la magnitud de origen y disipación respectivamente para la fase q. En un proceso de transferencia de masa interfase, uno de los dos términos es normalmente cero. Observe el siguiente ejemplo:
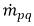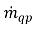y representan la magnitud de origen y disipación respectivamente para la fase q. En un proceso de transferencia de masa interfase, uno de los dos términos es normalmente cero. Observe el siguiente ejemplo:En un proceso de evaporación, la fase q líquida pierde masa, 
y 
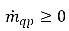, mientras en la fase de vapor, 
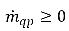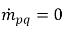y 
.
y 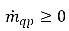, mientras en la fase de vapor, 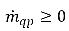y 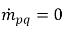.Para el sistema de n fases, la suma de fracciones volumétricas de fase satisface la restricción física:
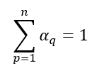
ecuación 2.58
O la conservación de masa total:
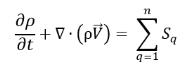
ecuación 2.59
donde las cantidades de la mezcla se definen a continuación:
◦ Volumen: densidad promedio de la mezcla
ecuación 2.60
◦ Masa: velocidad promedio de la mezcla
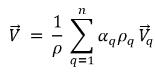
ecuación 2.61
• Ecuación del momento de la mezcla: se obtiene sumando las ecuaciones individuales del momento para todas las fases del sistema. En la ecuación 2.56, si se define 
, se obtiene
, se obtiene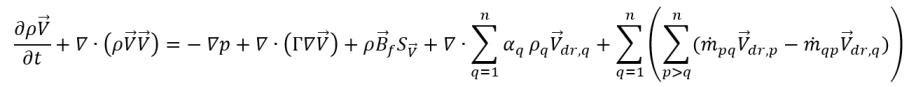
ecuación 2.62
donde las cantidades de la mezcla se definen a continuación:
◦ Volumen: viscosidad promedio de la mezcla.
ecuación 2.63
El coeficiente de difusión Γ en la ecuación 2.62 se calcula mediante la viscosidad dinámica μ y la viscosidad turbulenta μt de la mezcla. Los dos últimos términos del lado derecho representan la transferencia de momento directa y el intercambio de momento inducido por la transferencia de masa. Se determinan mediante las velocidades de desviación de fase, 
definidas como:
definidas como:
ecuación 2.69
En el método homogéneo, es posible modelar esta velocidad de desviación mediante un modelo algebraico. Sin embargo, en el modelo actual de VOF y mezcla, no se supone ningún deslizamiento entre las fases:
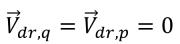
Por lo tanto, ambos términos de intercambio de momento son cero.
◦ Ecuación de energía de mezcla
Sin deslizamiento de velocidad, la ecuación de energía para la mezcla toma la siguiente forma:
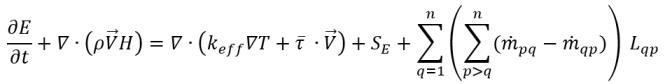
ecuación 2.70
donde las variables de la mezcla se definen a continuación:
▪ Volumen: conductividad promedio de calor
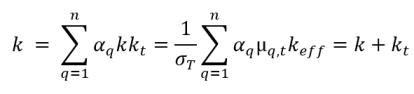
ecuación 2.71
▪ Masa: energía y entalpía promedio de la mezcla
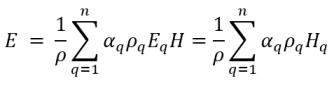
ecuación 2.72
En la ecuación 2.70 de energía de la mezcla, el término de calentamiento viscoso,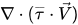 
, se calcula como en el flujo de una sola fase y SE es el origen de calor total externo o del usuario.
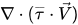, se calcula como en el flujo de una sola fase y SE es el origen de calor total externo o del usuario.El último término del lado derecho es la transferencia de calor de la interfaz producida por la transferencia de masa. Con la suposición de que las fases comparten la misma temperatura, Lgp depende de la definición de Hq y Hp en la ecuación de energía resuelta.
Como se describe en el módulo Calor, la entalpía estática de un material consta de dos partes: la entalpía de referencia de estado estándar y la entalpía sensible. Si se supone que la fase es líquida y la fase p es vapor, las entalpías estáticas totales de fase son las que se indican a continuación:
ecuación 2.73
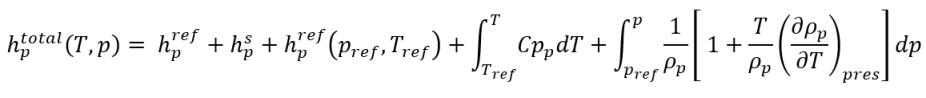
ecuación 2.74
donde,
pref | presión de referencia |
Tref | temperatura de referencia |
hq, ref | entalpías de referencia del estado estándar de la fase q |
hp,ref | entalpías de referencia del estado estándar de la fase p |
Diferencia de las entalpías de referencia
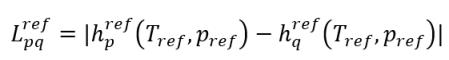
ecuación 2.75
es el calor latente a la temperatura Tref y la presión pref de referencia.
▪ Con inclusión de entalpía de referencia estándar:
En la ecuación 2.70, si la entalpía H es la entalpía total de la mezcla, se tiene
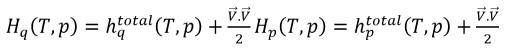
ecuación 2.76
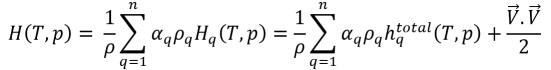
ecuación 2.77
La diferencia debida a las entalpías de formación de la fase o el calor latente Lpq ya se ha incluido en la ecuación de energía. La cantidad se define en cero:
Lpq=0
Y la transferencia de calor debida a la transferencia de masa, el último término del lado derecho en la ecuación 2.70, es cero en la ecuación de energía de la mezcla.
▪ Con exclusión de entalpía de referencia estándar:
En un solver CFD, la entalpía total no se resuelve directamente. En su lugar, solo se incluye la entalpía sensible relativa a la temperatura de saturación en la entalpía resuelta y la energía interna:
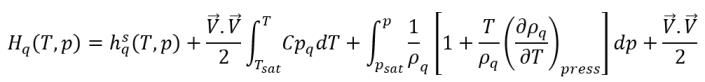
ecuación 2.79
ecuación 2.80
Lpq no es cero. Debe ser el calor latente:
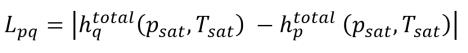
ecuación 2.81
donde,
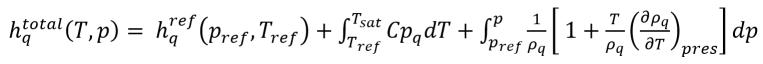
ecuación 2.82
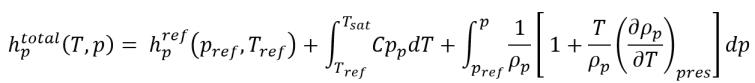
ecuación 2.83
En Creo Flow Analysis, por defecto, la entalpía de referencia de estado estándar se toma en consideración automáticamente. No se requiere ninguna entrada del usuario.
Modelos de turbulencia
• Modelos de turbulencia k-ε de la mezcla
En los modelos multifase de volumen de fluido (VOF) y mezcla, se tiene en cuenta el efecto de turbulencia en la mezcla de fases mediante la utilización de las extensiones de los modelos de turbulencia de una sola fase. Los modelos de turbulencia y los tratamientos próximos a la pared, descritos en el módulo Turbulencia, se extienden a los flujos multifase en Creo Flow Analysis. Con las cantidades de flujo de la mezcla, los modelos estándar y RNG k-ε tienen los mismos formatos generales que los modelos de turbulencia de una fase:
ecuación 2.84
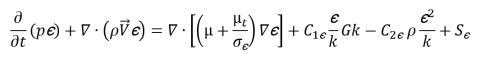
ecuación 2.85
donde la densidad de la mezcla ρ, la velocidad 
y la viscosidad molecular μ se calculan a partir de sus valores de fase respectivos utilizando relaciones en la ecuación 2.60, la ecuación 2.61 y la ecuación 2.63, respectivamente; Sk y Sε incluyen los orígenes externos y del usuario posibles, y los orígenes de interacción de fase. La viscosidad turbulenta para la mezcla, μt se calcula directamente con la expresión:
y la viscosidad molecular μ se calculan a partir de sus valores de fase respectivos utilizando relaciones en la ecuación 2.60, la ecuación 2.61 y la ecuación 2.63, respectivamente; Sk y Sε incluyen los orígenes externos y del usuario posibles, y los orígenes de interacción de fase. La viscosidad turbulenta para la mezcla, μt se calcula directamente con la expresión: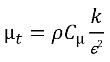
ecuación 2.86
mientras que la producción de energía cinética turbulenta se calcula en función de los gradientes de viscosidad y velocidad turbulentas de la mezcla:
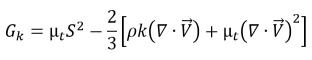
ecuación 2.87
donde S es el módulo de la velocidad de deformación promedio de la mezcla,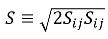 
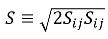
La viscosidad turbulenta para la fase q se puede calcular como se indica a continuación:
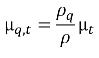
ecuación 2.87
• Efecto de difusión turbulenta
En los flujos turbulentos multifase, surge una fuerza turbulenta dispersa cuando se calcula el promedio del término de arrastre interfacial instantáneo, que actúa como el de la difusión de fase. Normalmente, el modelo euleriano de varios fluidos no homogéneos trata este efecto turbulento como una fuerza interfase adicional que se determina según los gradientes de fracciones volumétricas de fase en ecuaciones de momento de fase. Sin embargo, este efecto turbulento también se puede modelar directamente si se toma en consideración como un término de difusión turbulento en las ecuaciones de fracción volumétrica de fase. Al dividir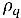 
y agrupar todos los orígenes como 
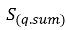(la suma de orígenes de transferencia de masa interfase y masa externa), se obtiene la siguiente ecuación gobernante para la fracción volumétrica de fase q en flujos turbulentos:
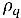y agrupar todos los orígenes como 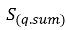(la suma de orígenes de transferencia de masa interfase y masa externa), se obtiene la siguiente ecuación gobernante para la fracción volumétrica de fase q en flujos turbulentos:
donde el primer término del lado derecho es el término de difusión turbulenta en la fase q, que debe cumplir la siguiente restricción para satisfacer la conservación de masa total:
Normalmente, los términos de difusión turbulenta se implementan como opción. No se incluyen por defecto.
Modelado de los límites multifase
En los modelos multifase de volumen de fluido (VOF) y mezcla, las condiciones de límite para las ecuaciones de flujo y energía son las mismas que las de los flujos de una sola fase. Estas se describen en los módulos Flujo y Calor. Para las fracciones volumétricas de fase, solo se aplican valores fijos y de gradiente cero en lo siguiente:
• Límite de entrada de n fases
Para (n-1) fases, las fracciones volumétricas de entrada están predeterminadas, mientras que la fase nth se obtiene mediante la restricción física:
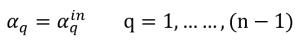
ecuación 2.88
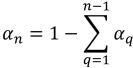
ecuación 2.89
Y la fracción volumétrica de cada fase debe ser no negativa.
• Salida, simetría y límite de pared
Para (n-1) fases, se aplican condiciones de gradiente cero para todos los límites de salida, simetría y pared, mientras que la fase nth se obtiene mediante la restricción física:
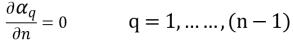
ecuación 2.90
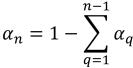
ecuación 2.91
Las anteriores ecuaciones gobernantes, los modelos de turbulencia y las condiciones de límite forman la base de los modelos multifase de VOF y mezcla homogéneos. Sin términos de origen externos o del usuario y transferencias de masa interfase, son un sistema de ecuaciones cerradas y se resuelven numéricamente mediante un solver multifase de volumen finito basado en la presión. Muchas aplicaciones prácticas requieren submodelos específicos, como la fuerza de la tensión de superficie en modelos de VOF y las transferencias de masa interfase, para capturar con precisión los procesos y fenómenos físicos respectivos. En lugar de aglomerar los submodelos en los orígenes externos o del usuario, se recomienda incluirlos directamente en los modelos integrados.