Modelos de cavitación
En Creo Flow Analysis, como en el modelo original de Singhal et al, se supone siempre que el fluido de trabajo de los flujos de cavitación es una mezcla de líquido, vapor y algunos gases no condensables. Por defecto, los modelos de cavitación se tienen en cuenta para el cambio de fase líquido-vapor y para el efecto de gases no condensables. En la siguiente tabla, se proporcionan cinco modelos diferentes para la predicción de la aireación y la cavitación en un sistema líquido, según el enfoque de modelado para el efecto de gas no condensable. Estos modelos se describen con detalle en esta sección.
|
Modelos para NCG
|
Descripción
|
|---|---|
|
Fracción másica de gas constante
|
La fracción másica de NCG (gas no condensable) es constante y se considera fuera de la solución con pequeñas burbujas compresibles.
|
|
Fracción másica de gas variable
|
Similar al modelo de fracción másica de gas constante, pero la fracción másica de NCG puede variar, por ejemplo, las entradas pueden introducir fracciones másicas diferentes.
|
|
Modelo de gas disuelto en equilibrio
|
La fracción másica del NCG disuelto en el líquido es igual al valor de equilibrio.
|
|
Modelo de gas disuelto
|
La fracción másica del NCG disuelto en el líquido depende de la velocidad de absorción o desorción y el valor de equilibrio.
|
|
Modelo de gas completo
|
Combina la fracción másica de gas variable y el modelo de gas disuelto.
|
Modelo de fracción másica de gas constante
El modelo de fracción másica de gas constante es el modelo de cavitación básico o por defecto en Creo Flow Analysis. Se basa en el trabajo de Singhal et al. En este modelo se supone que en el fluido de trabajo, el gas no condensable (NCG) que siempre está presente en el líquido, es un gas no disoluble o burbujas libres de gas que siguen la ley de los gases ideales. Aunque todos los gases no condensables descritos anteriormente se pueden expandir libremente con la disminución de la presión en las zonas de cavitación, la fracción másica de gases no condensables se describe con anterioridad y permanece igual en un flujo de cavitación:
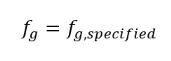
ecuación 2.217
donde fg,especificado es un valor definido por el usuario.
La densidad del gas no condensable sigue la ley de los gases ideales:
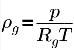
ecuación 2.218
donde T es la temperatura del fluido, que puede describirse previamente (flujo isotérmico) u obtenerse mediante la resolución de la ecuación 2.168 de conservación de la energía de la mezcla cuando se toma en consideración la transferencia de calor. De la ecuación 2.173, se deduce que la fracción volumétrica del gas no condensable es la siguiente:

ecuación 2.219
Aunque la fracción másica de NCG sea fija y tenga por lo general un valor pequeño de 1.5e-05 o 15 PPM en agua natural, su fracción volumétrica αg varía y puede tener un valor mayor. En cavidades o zonas de baja presión, el gas no condensable compite con el vapor para rellenar el vacío del espacio, según las densidades del gas y del vapor.
Respecto a la transferencia de masa líquido-vapor, la ecuación 2.194 y la ecuación 2.195 sirven de base para construir el origen de la cavitación y el término de disipación en la ecuación 2.169 de fracción másica de vapor. En concreto, el radio de la burbuja, RB se debe estimar con las cantidades de flujo conocidas durante la expansión y contracción de la burbuja. Singhal et al argumentó que si el tamaño de RB típico de burbuja es el mismo que el tamaño de burbuja límite (máximo posible), el valor de RB se determina mediante el equilibrio entre las fuerzas de arrastre aerodinámico y tensión de superficie. Una correlación que se utiliza en el sector nuclear es:
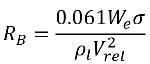
ecuación 2.220
donde Vrel es la magnitud de la velocidad relativa líquido-vapor. En el régimen de flujo con burbujas en el que se produce cavitación, Vrel es por lo general pequeño, aproximadamente entre un 5 y un 10 % de la velocidad del líquido. Mediante el uso de diferentes argumentos de límite, como RB →0 como αv →0, y el hecho de que las velocidades de cambio de fase por unidad de volumen deben ser proporcionales a las fracciones volumétricas (o fracciones másicas) de la fase contribuyente, se obtienen las siguientes expresiones para las velocidades de generación/condensación de vapor para completar el modelo de cavitación:
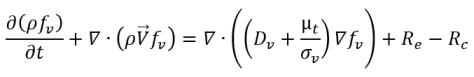
ecuación 2.221
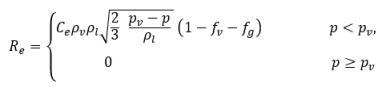
ecuación 2.222
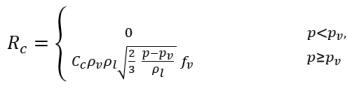
ecuación 2.223
donde Ce y Cc son los coeficientes de evaporación y condensación, que pueden ser valores constantes especificados por el usuario y que se definen por defecto en 1.0 o funciones de cantidades de flujo conocidas. En la ecuación 2.222 y la ecuación 2.223, se introduce una nueva presión umbral ρv para reemplazar la presión de vapor de saturación ρsat en la ecuación 2.194 y la ecuación 2.195. Según Singhal et al, para tener en cuenta el efecto de turbulencia en los flujos de cavitación, observado en investigaciones experimentales, un valor local de las fluctuaciones de presión turbulentas según Hinze:
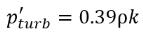
ecuación 2.224
se añade a la presión de vapor de saturación para elevar el valor de presión umbral de cambio de fase a:

ecuación 2.225
Para flujos laminares, pv=psat(T)
Cuando se toma en consideración la transferencia de calor y todas las densidades de fase, incluido el líquido, el vapor y los gases no condensables, están sujetas a cambios con la temperatura, la presión de vapor de saturación psat es también una función de temperatura. Por lo tanto, el efecto térmico directo sobre la cavitación se puede tomar en consideración en este modelo de cavitación.
Modelo de fracción másica de gas variable
En el modelo de fracción másica de gas variable se supone que el gas no condensable siempre permanece como gas libre que no se puede disolver en el líquido, pero la fracción másica deja de ser una constante descrita previamente como en el modelo de fracción másica de gas constante. En su lugar, la distribución de la fracción másica local se gobierna mediante una ecuación de transporte. Pero la transferencia de masa de líquido-vapor se modela por el mismo modelo de cavitación al que se hace referencia en la ecuación 2.221, la ecuación 2.222 y la ecuación 2.223. A continuación, se proporciona el conjunto completo de las ecuaciones de modelado para mayor claridad:
• Cambio de fase líquido-vapor
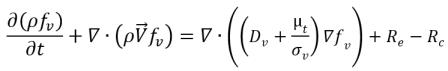
ecuación 2.226
donde:
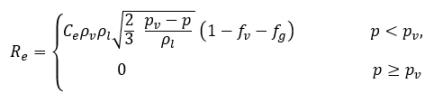
ecuación 2.227
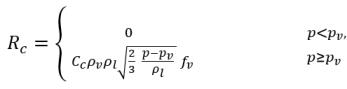
ecuación 2.228
• Ecuación de transporte de gas no condensable
Siguiendo la ecuación 2.199, la ecuación de transporte para el gas no condensable (fg) es:

ecuación 2.229
donde Sg es el origen externo o definido por el usuario para el gas no condensable.
Modelo de gas disuelto en equilibrio
En los flujos de cavitación, los gases no condensables del fluido se disuelven en un líquido o se liberan para conseguir un equilibrio dinámico de las concentraciones de masa entre las fases líquida y gaseosa. En el modelo de gas disuelto en equilibrio se supone que la fracción másica del gas no condensable total permanece como una constante. Sin embargo, una parte se disuelve en el líquido para satisfacer inmediatamente la condición de equilibrio local. Matemáticamente, además de la misma ecuación de fracción másica para vapor y modelos de transferencia de masa de vapor, se resuelve una ecuación de transporte adicional para la fracción másica del gas disuelto fgd, que se supone que siempre se encuentra en estado de equilibrio. Las ecuaciones de modelado son las siguientes:
• Cambio de fase líquido-vapor
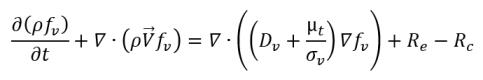
ecuación 2.230
donde:
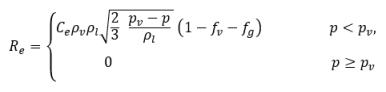
ecuación 2.231
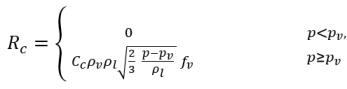
ecuación 2.232
• Absorción/disolución o liberación de gas
En la ecuación 2.197, la ecuación 2.211 y la ecuación 2.212, la ecuación de transporte de gas disuelto tiene el siguiente formato:
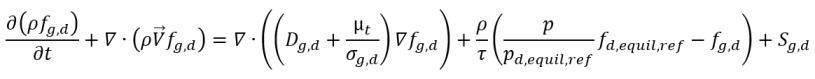
ecuación 2.233
donde:
Sg,d | ley definida por el usuario de disolución o liberación de gas |
fd,equil,ref | fracción másica en equilibro del gas disuelto en la presión de referencia pd,equil,ref |
fd,equil,ref y pd,equil,ref | valores especificados por el usuario |
En este modelo de equilibrio, la escala de tiempo Γ se aproxima a cero de modo que la transferencia de masa es casi instantánea. Se debe tener en cuenta que en la ecuación 2.231, el gas libre tiene la fracción másica fg,f, en lugar de fg. La fracción másica de gas libre se obtiene de la condición:
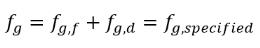
ecuación 2.234
donde fg,especificado es un valor definido por el usuario.
Modelo de gas disuelto
En este modelo se relaja la condición de que el gas disuelto en el líquido se debe encontrar siempre en estado de equilibrio. En lugar de venir determinada por la condición de equilibrio con transferencia de masa instantánea, la fracción másica de gas disuelto (fg,d) depende del transporte del componente y la velocidad de disolución o liberación (velocidad finita). Por lo tanto, el modelo de gas disuelto comparte las mismas formulaciones de modelado que el modelo de gas disuelto en equilibrio, ecuación 2.230ecuación 2.234. Sin embargo, las velocidades finitas de transferencia de masa para la disolución y la liberación de gas se caracterizan por las escalas de tiempo diferentes (Γ). Para la absorción de gas o la disolución en el líquido, Γ se da por un tiempo de absorción especificado (el tiempo de disolución del gas disuelto por defecto es 10 s). Para la liberación de gas disuelto del líquido, la velocidad de transferencia de masa viene establecida por un tiempo de liberación de gas especificado (el tiempo de liberación de gas disuelto por defecto Γ es 10 s).
Modelo de gas completo
El modelo de gas completo es una combinación del modelo de gas disuelto y el modelo de gas variable. La fracción másica del gas no condensable está sujeta a cambio con el tiempo y el espacio, mientras que la disolución o la absorción y la liberación de gas también se pueden producir para los gases no condensables. A continuación, se proporciona el conjunto completo de ecuaciones de modelado:
• Cambio de fase líquido-vapor
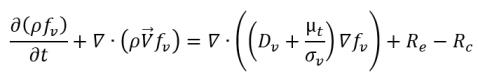
ecuación 2.235
donde:
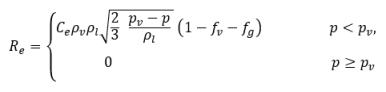
ecuación 2.236
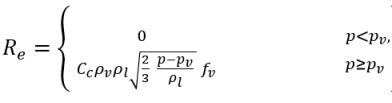
ecuación 2.237
• Transporte de gas no condensable
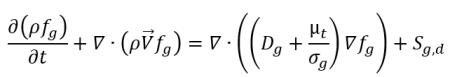
ecuación 2.238
• Disolución o liberación de gas
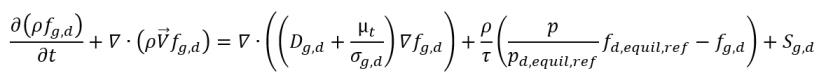
ecuación 2.239