Teoría de los modelos de cavitación
En la ecuación 2.169 de transporte de vapor, Re y Rc son los términos de origen de transferencia de masa conectados a la expansión y contracción de las burbujas de vapor en flujos de cavitación. Estos términos se tienen en cuenta para el intercambio de masa entre las fases vapor y líquido durante un proceso de cavitación. Re y Rc se modelan en la ecuación de Rayleigh-Plesset que describe la expansión de una única burbuja de vapor en un líquido.
Transferencia de masa de líquido-vapor
Para derivar una expresión de la velocidad neta de cambio de fase en cavitación, considere un flujo incompresible de dos fases líquido-vapor con una velocidad de deslizamiento cero donde el gas no condensable no se tiene en cuenta. Si se introduce R para representar la velocidad neta de la transferencia de masa líquido a vapor, se obtienen las ecuaciones de fracción volumétrica de líquido y vapor, así como la ecuación de continuidad de masa total, que se indican a continuación:
• Fase de líquido
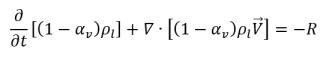
ecuación 2.179
• Fase de vapor
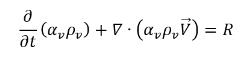
ecuación 2.180
• Mezcla (continuidad de masa total)
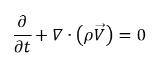
ecuación 2.181
En el sistema de dos fases líquido-vapor, la densidad de la mezcla ρ se puede expresar en términos de las densidades de fracción volumétrica de vapor y de fase:
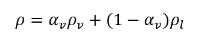
ecuación 2.182
Puesto que las densidades de líquido y vapor se suponen constantes (incompresibles), se deriva una relación entre el gradiente de velocidad y la fracción volumétrica de vapor de la ecuación 2.181 y la ecuación 2.182:
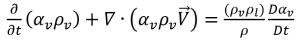
ecuación 2.183
La combinación de la ecuación 2.179 y la ecuación 2.183 proporciona la expresión para el término de origen de masa neta como:
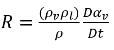
ecuación 2.184
Mediante la sustitución de la ecuación 2.184 por la ecuación 2.180, la ecuación para la fracción volumétrica de vapor se reformula con el formato general:
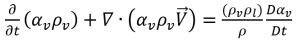
ecuación 2.185
Con la aplicación de la relación entre la fracción másica y la fracción volumétrica de la ecuación 2.173 de vapor, se obtiene la ecuación 2.185 en términos de fracción másica de vapor:
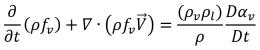
ecuación 2.186
De la ecuación 2.185 y la ecuación 2.186 se entiende que bajo la condición de deslizamiento de velocidad cero entre la fase líquido y vapor, la cavitación se modela como un flujo de una sola fase con una ecuación de transporte de fracción másica de vapor adicional o como un flujo de mezcla multifase euleriano con transferencia de masa líquido-vapor. Sin tener en cuenta el efecto de la diferencia de velocidad de difusión y fase, los dos métodos son idénticos matemáticamente. Creo Flow Analysis utiliza el método de una sola fase para modelar los flujos de cavitación.
Consideración de la dinámica de las burbujas
Para la mayoría de los fenómenos naturales y sistemas de ingeniería, hay un número suficiente de núcleos como, por ejemplo, burbujas, gases no condensables, etc., en el líquido para el inicio de la cavitación. Por lo tanto, para modelar el proceso de cavitación, el foco se debe colocar principalmente en tener en cuenta de forma correcta la expansión y la contracción de las burbujas. Si se presupone que en un líquido que fluye hay deslizamiento de velocidad cero entre el líquido y las burbujas de vapor, la ecuación de la dinámica de las burbujas se deriva de la ecuación generalizada de Rayleigh-Plesset que describe la expansión de una burbuja de gas en un líquido:
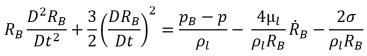
ecuación 2.187
donde,
RB | radio de la burbuja |
pB | presión en la burbuja (se supone que es la presión de vapor a la temperatura del líquido en ausencia de otros gases) |
p | presión en el líquido que rodea a la burbuja |
σ | coeficiente de tensión de superficie entre el líquido y el vapor |
Esta ecuación se deriva del equilibrio mecánico (sin barreras térmicas para la expansión de la burbuja).
Si se hace caso omiso del segundo derivado de tiempo (adecuado para bajas frecuencias de oscilación), el término de amortiguación viscosa y la fuerza de la tensión de superficie, se obtiene una expresión reducida de la ecuación 2.187 que es válida para el estado asintótico:
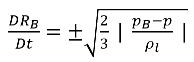
ecuación 2.188
Esta ecuación de Rayleigh-Plesset reducida proporciona un método físico para introducir los efectos de la dinámica de las burbujas en los modelos de cavitación. El radio de la burbuja puede aumentar o disminuir en función de los signos de (pB–p): la burbuja se expande si p<pB y se contrae cuando p>pB. Por lo tanto, la ecuación 2.188 se reescribe de la siguiente manera:
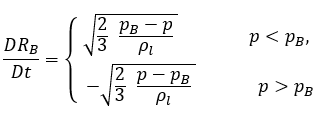
ecuación 2.189
Si η es la densidad del número de burbujas de vapor en un líquido (el número de burbujas presentes por unidad de volumen) y todas las burbujas de vapor son esferas perfectas con el mismo radio RB, la fracción volumétrica de la fase de vapor es la que se indica a continuación:
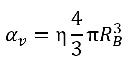
ecuación 2.190
Se supone que las burbujas de vapor no se pueden crear ni destruir en un líquido, pero que las burbujas pueden expandirse (evaporación) y contraerse (condensación) durante un proceso de cavitación. En la ecuación 2.190, la densidad del número de burbujas de vapor (η) permanece constante, pero el radio de la burbuja (RB) aumenta o disminuye. El tiempo derivado de la fracción volumétrica de vapor se calcula de la siguiente manera:
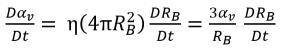
ecuación 2.191
Mediante la sustitución de la ecuación 2.191 por la ecuación 2.186 se obtiene la ecuación de transporte que gobierna la fracción másica de la fase de vapor:
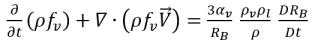
ecuación 2.192
Con la aplicación de la ecuación 2.189, la velocidad neta de transferencia de masa por unidad de volumen entre el líquido y el vapor tiene el siguiente formato:
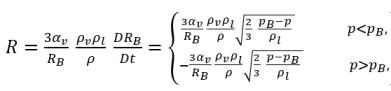
ecuación 2.193
donde la ecuación 2.193 indica que en la cavitación, la velocidad de transferencia de masa por unidad de volumen (R) es la función (proporcional) de la densidad de la fase vapor y líquido, además de ser también inversamente proporcional a la densidad de la mezcla. Puesto que la ecuación 2.192 se deriva directamente de las continuidades de masa de mezcla y fase, es exacta y debe representar con precisión la transferencia de masa entre la fase líquido y vapor en la cavitación. Con la introducción de la dinámica de las burbujas, la ecuación 2.193 utiliza el método similar para modelar dos procesos de transferencia de masa opuestos y físicamente diferentes: de líquido a vapor (expansión o evaporación de las burbujas) y de vapor a líquido (contracción o condensación de las burbujas). Para la ecuación 2.192 de transporte de fracción másica de vapor, la expansión de las burbujas es un término de origen, mientras que la contracción de las burbujas se trata como un término de disipación.
En modelos prácticos de cavitación, la presión p del campo lejano local se considera normalmente la misma que la presión del centro de la celda. La presión de burbuja pB es igual a la presión de vapor de saturación (psat, una propiedad del material) en ausencia de gases disueltos, transporte de masa y amortiguación viscosa, pB=psat
Si se comparan la ecuación 2.192 y la ecuación 2.193 con la ecuación 2.169 de fracción másica de vapor general, los términos de origen Re y Rc son los siguientes:
• Si la presión de flujo local se encuentra por debajo de la presión de vapor de saturación, p<psat, solo se produce evaporación, de modo que:
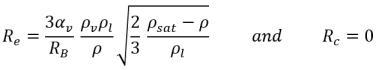
ecuación 2.194
• Si la presión de flujo local se encuentra por encima de la presión de vapor de saturación, p>psat, solo se produce condensación:
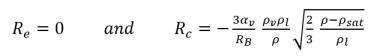
ecuación 2.195
La ecuación 2.194 y la ecuación 2.195 forman la base de casi todos los modelos de cavitación de dos fases mecánicas disponibles. Creo Flow Analysis ha utilizado el enfoque de modelado de Singhal et al.
Absorción/disolución y liberación de gas
A menudo, en un fluido de trabajo hay gases no condensables que pueden tener un impacto significativo en la cavitación. A veces, un gas no condensable se transporta libremente con el flujo y también se disuelve en un líquido o se libera, con la finalidad de lograr de forma natural un equilibrio dinámico de las concentraciones de masa entre las fases líquido y gas. La absorción y la disolución de gas, así como su liberación, en un líquido es también un fenómeno de transferencia de masa de líquido-gas, gobernado por las diferencias y gradientes de la concentración de masa. Para modelar los flujos de cavitación es necesario tener en cuenta también el efecto del gas no condensable y la posible transferencia de masa de líquido-gas en el flujo de la mezcla.
Si se presupone que en un flujo de dos fases de líquido-gas, existe un gas no condensable, como el aire o el oxígeno, tanto en la fase de líquido (gas disuelto) como en la fase de gas (gas libre), las ecuaciones de transporte de fracción másica de gas en cada fase son las siguientes:
• Gas libre (fase de gas)
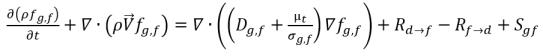
ecuación 2.196
• Gas disuelto (fase de líquido)
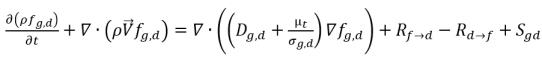
ecuación 2.197
donde,
fg,f | fracciones másicas del gas libre |
fg,d | fracciones másicas del gas libre y gas disuelto, |
Sg,f, Sg,d | orígenes externos o definidos por el usuario. |
Dg,f | difusividad del gas libre y el gas disuelto |
Dg,d | difusividad del gas disuelto |
Si la fracción másica de un gas no condensable se describe con anterioridad como fg, se obtiene:
fg=fg,f
o su transporte en el espacio y tiempo se obtiene resolviendo la siguiente ecuación:
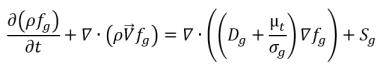
ecuación 2.199
Se debe tener en cuenta que para la ecuación 2.196, la ecuación 2.197 y la ecuación 2.199 solo se deben resolver directamente dos de ellas.
En la ecuación 2.196 y la ecuación 2.197, el origen Rd→f indica la velocidad de liberación del gas disuelto y Rf→d indica la velocidad de absorción o de disolución del gas libre.
Cuando las dos fases están en contacto, existe la tendencia de que el gas libre f y el gas disuelto d se transporten de una fase a la otra para conseguir un equilibrio dinámico entre las dos fases. En los modelos de equilibrio se supone que las velocidades volumétricas de las transferencias de masa dependen de los gradientes o las diferencias de concentración de masa:
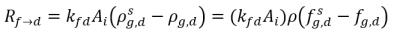
ecuación 2.200
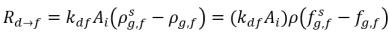
ecuación 2.201
donde,
AI | área interfacial de líquido-gas |
kf,d(=kd,f) | coeficiente de transferencia de masa volumétrica en bloque |
ρg,d(=ρfg,d) | concentraciones de masa locales de gas disuelto |
ρg,f(=ρfg,f) | concentraciones de masa locales de gas libre |
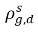 | concentraciones de masa en equilibrio del gas disuelto en las fases de alojamiento |
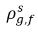 | concentraciones de masa en equilibrio del gas libre en las fases de alojamiento |
Se debe tener en cuenta que 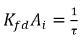 tiene la unidad de tiempo inverso, 1/s, un indicador de la eficacia de transferencia de masa. Por lo tanto, la ecuación 2.200 y la ecuación 2.201 también tienen los siguientes formatos:
tiene la unidad de tiempo inverso, 1/s, un indicador de la eficacia de transferencia de masa. Por lo tanto, la ecuación 2.200 y la ecuación 2.201 también tienen los siguientes formatos:
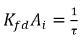 tiene la unidad de tiempo inverso, 1/s, un indicador de la eficacia de transferencia de masa. Por lo tanto, la ecuación 2.200 y la ecuación 2.201 también tienen los siguientes formatos:
tiene la unidad de tiempo inverso, 1/s, un indicador de la eficacia de transferencia de masa. Por lo tanto, la ecuación 2.200 y la ecuación 2.201 también tienen los siguientes formatos: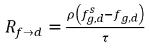
ecuación 2.202
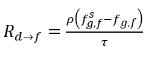
ecuación 2.203
Normalmente, 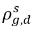 y
y 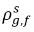 no son iguales (discontinuidad). Existe una curva de equilibrio claramente definida entre las dos concentraciones, que depende de la temperatura, la presión y las composiciones de la mezcla. La curva es normalmente monotónica y no lineal, y se expresa a menudo como una relación cuasi lineal con el coeficiente
no son iguales (discontinuidad). Existe una curva de equilibrio claramente definida entre las dos concentraciones, que depende de la temperatura, la presión y las composiciones de la mezcla. La curva es normalmente monotónica y no lineal, y se expresa a menudo como una relación cuasi lineal con el coeficiente 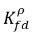
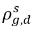 y
y 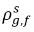 no son iguales (discontinuidad). Existe una curva de equilibrio claramente definida entre las dos concentraciones, que depende de la temperatura, la presión y las composiciones de la mezcla. La curva es normalmente monotónica y no lineal, y se expresa a menudo como una relación cuasi lineal con el coeficiente
no son iguales (discontinuidad). Existe una curva de equilibrio claramente definida entre las dos concentraciones, que depende de la temperatura, la presión y las composiciones de la mezcla. La curva es normalmente monotónica y no lineal, y se expresa a menudo como una relación cuasi lineal con el coeficiente 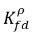
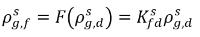
ecuación 2.204
donde Kf,d se decide normalmente mediante leyes físicas o correlaciones empíricas. Un enfoque común es seguir la ley de Henry que proporciona una relación generalizada de equilibrio. Esto indica que para una mezcla de líquido en contacto con la fase de gas, la presión parcial de gas libre ρg,f es igual al producto de la fracción molar en equilibrio del gas disuelto en la fase de líquido, 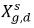 y la constante de Henry, Hx:
y la constante de Henry, Hx:
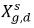 y la constante de Henry, Hx:
y la constante de Henry, Hx: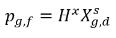
ecuación 2.205
Si la fase de gas libre sigue la ley de los gases ideales, la ley de Dalton de presión parcial ofrece la siguiente ecuación:
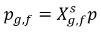
ecuación 2.206
Si se utiliza ecuación 2.204 - la ecuación 2.206, se genera la siguiente relación de equilibrio:
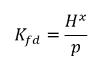
ecuación 2.207
Por lo tanto, la constante de Henry tiene una unidad de presión y se puede considerar como presión de referencia. Suponiendo que, para una mezcla de líquido ideal en contacto con un gas, la constante de Henry es la presión de vapor de saturación psat, la ecuación 2.207 también es la siguiente:
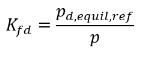
ecuación 2.208
donde pd,equil,ref es la presión de referencia para la fracción másica en equilibro del gas disuelto. Luego la ecuación 2.204 se reescribe como:
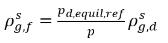
ecuación 2.209
En la ecuación 2.202 y la ecuación 2.203, 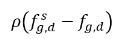 y
y 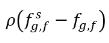 son las diferencias/gradientes de la concentración de masa, las fuerzas gobernantes de la absorción/disolución y la liberación de los gases no condensables. Indica que el transporte de gas no condensable a través de dos fases requiere la salida de la concentración de masa del estado de equilibrio. La dirección de la transferencia de masa mueve el sistema hacia el equilibrio según las concentraciones de masa local y en equilibrio en ambas fases. A partir del modelo de equilibrio, se extrae lo siguiente:
son las diferencias/gradientes de la concentración de masa, las fuerzas gobernantes de la absorción/disolución y la liberación de los gases no condensables. Indica que el transporte de gas no condensable a través de dos fases requiere la salida de la concentración de masa del estado de equilibrio. La dirección de la transferencia de masa mueve el sistema hacia el equilibrio según las concentraciones de masa local y en equilibrio en ambas fases. A partir del modelo de equilibrio, se extrae lo siguiente:
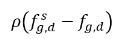 y
y 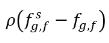 son las diferencias/gradientes de la concentración de masa, las fuerzas gobernantes de la absorción/disolución y la liberación de los gases no condensables. Indica que el transporte de gas no condensable a través de dos fases requiere la salida de la concentración de masa del estado de equilibrio. La dirección de la transferencia de masa mueve el sistema hacia el equilibrio según las concentraciones de masa local y en equilibrio en ambas fases. A partir del modelo de equilibrio, se extrae lo siguiente:
son las diferencias/gradientes de la concentración de masa, las fuerzas gobernantes de la absorción/disolución y la liberación de los gases no condensables. Indica que el transporte de gas no condensable a través de dos fases requiere la salida de la concentración de masa del estado de equilibrio. La dirección de la transferencia de masa mueve el sistema hacia el equilibrio según las concentraciones de masa local y en equilibrio en ambas fases. A partir del modelo de equilibrio, se extrae lo siguiente:◦ Absorción/disolución en un líquido: la transferencia de masa se produce de la fase de gas (gas libre) a la fase de líquido (gas disuelto). En el modelo de equilibrio se supone que el gas libre en la fase de gas se encuentra en estado de equilibrio: 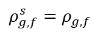 . Con la ecuación 2.204 y la ecuación 2.209, se obtiene lo siguiente:
. Con la ecuación 2.204 y la ecuación 2.209, se obtiene lo siguiente:
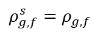 . Con la ecuación 2.204 y la ecuación 2.209, se obtiene lo siguiente:
. Con la ecuación 2.204 y la ecuación 2.209, se obtiene lo siguiente: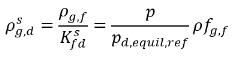
ecuación 2.210
De la ecuación 2.202 y la ecuación 2.203, se deriva que los términos de origen de transferencia de masa son:
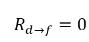
ecuación 2.211
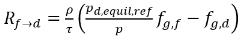
ecuación 2.212
◦ Liberación de gas de un líquido: la transferencia de masa se produce de la fase de líquido (gas disuelto) a la fase de gas (gas libre). En este proceso, en el modelo de equilibrio se supone que el gas disuelto en la fase de líquido se encuentra siempre en estado de equilibrio: 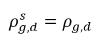 . De la ecuación 2.202, la ecuación 2.203, la ecuación 2.204 y la ecuación 2.209, se deriva que las velocidades de las transferencias de masa son las siguientes:
. De la ecuación 2.202, la ecuación 2.203, la ecuación 2.204 y la ecuación 2.209, se deriva que las velocidades de las transferencias de masa son las siguientes:
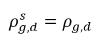 . De la ecuación 2.202, la ecuación 2.203, la ecuación 2.204 y la ecuación 2.209, se deriva que las velocidades de las transferencias de masa son las siguientes:
. De la ecuación 2.202, la ecuación 2.203, la ecuación 2.204 y la ecuación 2.209, se deriva que las velocidades de las transferencias de masa son las siguientes: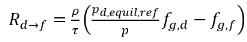
ecuación 2.213
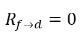
ecuación 2.214
Se debe tener en cuenta que cuando se disuelve una parte del gas no condensable en el líquido, el gas libremente expandible es solo la parte que queda en la fase de gas, fg,f. Por lo tanto la densidad de la mezcla se calcula como:
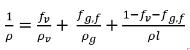
ecuación 2.215
y la fracción volumétrica del gas libre es la siguiente:
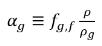
ecuación 2.216