ソルブブロック内の偏微分方程式
pdesolve(u, x, xrange, t, trange, [xpts], [tpts]) - n 次微分方程式の n 個の独立等式制約条件を含む、1 次元非線形偏微分方程式 (PDE) または連立偏微分方程式の解を求める、関数または関数のベクトル u(x,t) を返します。値は、線の数値法を使用して計算された解の点の行列から補間されます。
ソルブブロックで pdesolve を使用しなければなりません。
引数
• u は、ソルブブロック内に表示される、スカラー関数名または関数名のベクトル (変数名は含まれていない) です。たとえば、関数 f(x,t) および g(x,t)を解く場合、u は次のようになります。

下付き文字の偏微分表記に対応するため、関数の命名時にリテラル下付き文字を使用することはできません。
• x は空間変数名です。
• xrange は、x の実数境界値を含んでいる 2 要素の列ベクトルです。
• t は時間変数名です。
• trange は、t の実数境界値を含んでいる 2 要素の列ベクトルです。
• xpts (オプション) は、空間離散化点の数を表す整数です。
• tpts (オプション) は、時間的離散化点の数を表す整数です。
ソルブブロックの定義の一般的な規則が適用されます。ブロックのボディ内:
不明な関数
関数は、その変数について定義しなければなりません。たとえば、u ではなく u(x,t) を使用します。ソルブブロック内の偏微分を示すには、以下のいずれかを使用します。
• 下付き文字表記。たとえば、uxx(x,t) は x についての u の 2 次偏微分です。
下付き文字表記はソルブブロック内の pdesolve でのみ使用でき、ワークシートのほかの領域では使用できません。 |
• 偏微分演算子。
PDE 方程式
方程式は、論理演算子を使用して定義しなければなりません。2 次偏微分は方程式の左辺では使用できません。1 次微分でのみ方程式を連立方程式に変換できます。
境界条件
未知の各関数ごとに、初期条件 u(x,0)、および n 境界条件 (n は PDE の順序) が必要です。境界条件のタイプはディリクレ (u(0,t) = f(t)) またはノイマン (ux(0,t)=g(t)) で、空間積分範囲のいずれかの終点で指定できます。境界条件で使用される終点は、ode/pdesolve コマンドで指定した終点と一致していなければなりません。Mathcad は、制約条件のタイプと数が正しいことをチェックし、正しくない場合はエラーメッセージで警告します。
制約条件
フォーム u(x,t)+v(x,t)+w(x,t)=0 の代数制約条件を使用できます。これにより、さらに 1 つの未知の関数 w がシステムに追加されます。これは、ode/pdesolve 呼び出しの出力関数の 1 つとして指定しなければなりません。不等式制約条件は使用できません。
• pdesolve 関数の出力を関数名、または関数名のベクトルに割り当てます。
• 偏微分に使用する近似方法を変更するには、pdesolve 関数を右クリックし、別の方法を選択します。これは計算時間に影響を与える可能性があります。
• 線の数値法は、逆双曲線偏微分方程式と放物線型偏微分方程式、および部分的代数方程式を解くためにのみ適しています。プログラムループ内の方程式を解くには、numolを使用します。ポアソンの方程式などの楕円型偏微分方程式を解くには、Relax または Multigridを使用します。
pdesolve の操作中に発生する可能性のあるエラーと解決策のリストを以下に示します。
• エラー: この関数は少なくとも 5 つの引数を必要としますが、4 つに適用されています。
例:
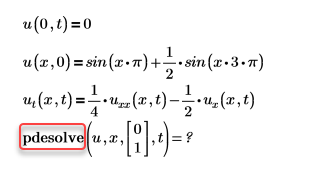
解決策: 欠落している引数 (ここでは trange) を追加します。
• エラー: この関数は最大 7 つの引数を受け入れますが、8 つに適用されています。
例:

解決策: 不要な引数を除去します。引数に関する詳細を参照してください。
• エラー: 時間変数の境界のベクトルの形式が正しくありません。
例:

解決策: trange が正しく定義されていません。引数の詳細を参照してください。
• エラー: 空間変数の境界のベクトルの形式が正しくありません。
例:

解決策: xrange が正しく定義されていません。引数の詳細を参照してください。
• エラー: 未知の関数名が正しく指定されていません。
例:

解決策: この関数は引数なしで表示される必要があります。
• エラー: 4 より大きい整数でなければなりません。
例:

または
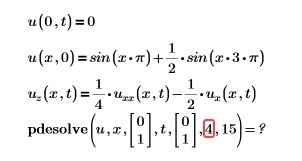
解決策: 離散化点の数は 4 より大きい整数でなければなりません。