微分演算子とプライム演算子
|
演算子
|
説明
|
キーボードショートカット
|
|---|---|---|
 |
f(t) の点 t における t についての n 次微分係数を返します。
• 数値評価の場合、n は 0 以上 5 以下の自然数です。
• シンボリック評価の場合、n は任意の自然数です。
|
Ctrl + Shift + D
|
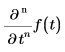 |
f(t) の点 t における t についての n 次偏微分係数を返します。
• 数値評価の場合、n は 0 以上 5 以下の自然数です。
• シンボリック評価の場合、n は任意の自然数です。
|
Ctrl + D
|
 |
関数 g を関数 f(t) の 1 次導関数として定義します。
• n 個のプライム演算子のカスケードにより、nth 導関数を得ることができます。
• 数値評価またはシンボリック評価に、任意の数のプライム演算子を使用できます。ただし、シンボリック評価の計算時間は大幅に短縮されます。
|
Ctrl + ' (アポストロフィ)
|
オペランド
• f(t) はスカラー値関数です。この関数は複素関数でもかまいません。
◦ 微分演算子の場合、f(t) 関数は任意の数の変数をとることができます。
◦ プライム演算子の場合、f(t) 関数の変数は 1 つのみにする必要があります。
• g は関数名です。
• t は微分する点です。
追加情報
• 式の 1 次微分係数を求める場合、微分演算子の指数プレースホルダーには何も入力しません。
• 微分する点が関数の特異点の近傍になければ、1 次微分係数は有効桁数 7 桁または 8 桁まで正確です。微分の次数が 1 つ上がるごとに有効桁数が約 1 桁減ります。
• 微分係数の計算に使用される数値解法は、Ridder 法の応用で、色々なステップサイズで (n + 1) 個の点で分割した差分を計算します (ここで、n は微分の次数)。さらに加重平均を使って、テーブル内の逐次近似を計算します。テーブルの値が逐次比較され、誤差項が許容誤差以下の場合に、一番誤差項の少なかった値が、微分係数として返されます