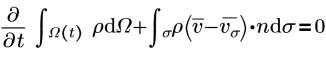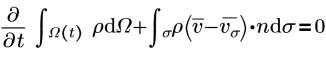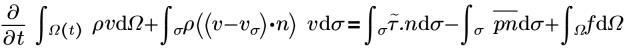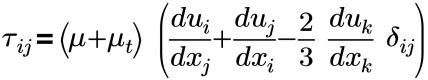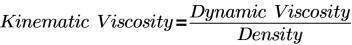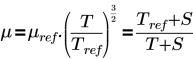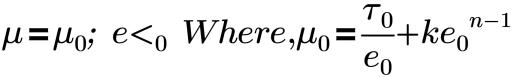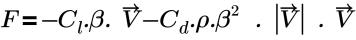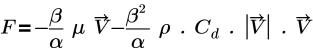Modèles de flux
Le module
Flux (Flow) calcule la conservation de la masse et l'
énergie cinétique à l'aide des équations de Navier-Stokes transitoires. Source :
H. Ding, F.C. Visser, Y. Jiang et M. Furmanczyk, "Demonstration and Validation of a 3-D CFD Simulation Tool Predicting Pump Performance and Cavitation for Industrial Applications", FEDSM2009-78256, 2009..
La forme intégrale (conservatrice) des équations de Navier-Stokes moyennées (RANS, Reynold's Averaged Navier-Stokes) est la suivante :
• Continuité
• Energie cinétique
• Tenseur de contrainte
où,
τij | contrainte de cisaillement effective (moléculaire + turbulente) |
f | force s'exerçant dans la masse du fluide |
n | normale à la surface |
ρ | pression statique (Pa) |
t | temps |
v | vitesse du fluide |
vσ | vitesse de maillage |
Ω(t) | volume de contrôle en tant que fonction du temps |
r | densité du fluide locale moyenne (kg/m3) |
σ | surface du volume de contrôle |
µ | viscosité dynamique (poiseuille ou Pa-s) |
µt | viscosité dynamique turbulente |
δij | delta de Kronecker (=1 pour i=j, =0 pour i≠j) |
Modèles de viscosité
• Constant Dynamic Viscosity : spécifie la
viscosité du fluide dans un volume sélectionné. La viscosité dynamique est exprimée en Pa-s ou en N-s/m
2.
La valeur de la viscosité dynamique est spécifiée dans la zone située sous la sélection Constant Dynamic Viscosity.
• Constant Kinematic Viscosity : spécifie la
viscosité du fluide dans un volume sélectionné. La viscosité cinématique est exprimée en m
2/s. La valeur de la viscosité cinématique est spécifiée dans la zone située sous la sélection
Constant Kinematic Viscosity.
• Sutherland Law : spécifie la
viscosité du fluide dans un volume sélectionné en termes de viscosité dynamique (Pa-s). L'équation et les entrées sont les suivantes :
où,
T | température (K) |
µref | viscosité à la température de référence (Pa-s) |
S | température de Sutherland (K) |
|  T est la température du fluide (K) requise en tant qu'entrée si le module d'énergie n'est pas actif. |
La loi de Sutherland permet de calculer la viscosité d'un gaz parfait sous la forme d'une fonction de la température. Source :
Sutherland, W. (1893), "The viscosity of gases and molecular force", Philosophical Magazine, S. 5, 36, pp. 507-531 (1893). Le tableau ci-après indique la température constante de Sutherland et la température de référence pour les gaz sélectionnés. Source :
en.wikipedia.org/wiki/viscosity.
Gaz | S (K) | Tref (K) | mref (Pa-s) |
air | 120 | 291.15 | 18.27 e-6 |
azote | 111 | 300.55 | 17.81 e-6 |
oxygène | 127 | 292.25 | 20.81 e-6 |
dioxyde de carbone | 240 | 293.15 | 14.8 e-6 |
monoxyde de carbone | 118 | 288.15 | 17.2 e-6 |
hydrogène | 72 | 293.85 | 8.76 e-6 |
ammoniac | 370 | 293.15 | 9.82 e-6 |
dioxyde de soufre | 416 | 293.65 | 12.54 e-6 |
hélium | 79.4 | 273 | 19 e-6 |
Modèles de viscosité non newtoniens
Les modèles de viscosité non newtoniens sont les suivants :
• modèle de Herschel-Bulkley ;
• modèles de Bingham.
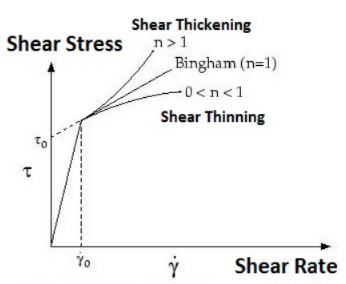
Ces modèles fournissent la viscosité appropriée pour les différents types de fluides qui présentent des propriétés de flux non newtonien. Le modèle de Herschel-Bulkley et les modèles de Bingham relient la contrainte de cisaillement au taux de cisaillement de la façon suivante :
où,
e0 | taux de cisaillement critique |
k | indice de cohérence |
τ0 | limite élastique du fluide |
n | indice de loi de la puissance ; pour le modèle de Bingham, n=1 |
|  Le taux de cisaillement de 0 est identique au point gamma dans le tracé ci-dessus. |
Resistance Model
L'option
Resistance Model du module
Flux (Flow) vous permet de définir une résistance dans un volume sélectionné. Le
Resistance Model comporte les deux modèles suivants :
• Pressure Loss : modèle basé sur l'équation suivante :
où,
Cl | coefficient de traînée linéaire (Pa-s/m2) |
Cd | coefficient de traînée quadratique (1/m) |
β | porosité |
ρ | masse volumique |
• Darcy's Law : modèle basé sur l'équation suivante :
où,
β | porosité |
α | perméabilité |
µ | viscosité dynamique |
V | vitesse |
Cd | coefficient de traînée quadratique (1/m) |
La vitesse utilisée dans l'équation de résistance correspond à la vitesse locale. La valeur F dans l'équation est exprimée en N/m3, telle que force/volume, gradient de pression (Dp/Dx) ou rg. La chute de pression dans l'interface est calculée en multipliant F par une épaisseur finie. La porosité est définie dans le module Commun (Common).