解題指令群中的偏微分方程式
pdesolve(u, x, xrange, t, trange, [xpts], [tpts]) - 傳回函數或函數 u(x,t) 向量,可求解具有 n 獨立等式條件約束之第 n 階微分方程式的一維非線性偏微分方程式 (PDE) 或 PDE 系統。值會從使用線性數值方法計算的解點矩陣內插。
您必須在解題指令群中使用 pdesolve 。
引數
• u 是純量函數名稱,或函數向量名稱 (不含變數名稱),它們會顯示在解題指令群中。例如,如果您要求解函數 f(x,t) 與 g(x,t),則 u 會是:
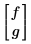
為了容納下標篇微分標記法,您無法在命名函數時使用 文字下標 。
• x 是空間變數名稱。
• xrange 是包含 x 之實數邊界值的雙元素欄向量。
• t 是時間變數名稱。
• trange 是包含 t 之實數邊界值的雙元素欄向量。
• xpts (選用) 是空間分隔點的整數。
• tpts (選用) 是時間分隔點的整數。
適用於定義解題指令群的一般規則。在區塊主體內:
未知函數
函數必須根據其變數加以定義。例如,使用 u(x,t) 而非 u。若要指示解題指令群中的偏導數,請使用下列其中一項:
• 下標標記法。例如,uxx(x,t) 是相對於 x 的第二個 u 偏導數。
下標標記法僅可用於解題指令群中的 pdesolve,無法用於工作表的其他區域。 |
• 偏導數運算子。
PDE 方程式
方程式必須使用布林等號來定義。方程式的左側不允許使用第二個偏導數,您只能在第一個偏導數中將方程式轉換方程式系統。
邊界條件
每個未知函數均必須有初始條件 u(x,0) 與 n 邊界條件,其中 n 是 PDE 的階數。邊界條件可以是狄里克雷 (u(0,t) = f(t)) 或紐曼 (ux(0,t)=g(t)) 類型,且可在空間積分範圍的任一端點指定。邊界條件中使用的端點必須符合 ode/pdesolve 指令中指定的端點。Mathcad 會檢查條件約束的類型與數目是否正確,並以錯誤訊息標示錯誤。
條件約束
允許 u(x,t)+v(x,t)+w(x,t)=0 形式的代數條件約束。如此會將額外的未知函數 w 新增至系統,此函數必須指定為 ode/pdesolve 呼叫中的其中一個輸出函數。不允許不等式條件約束。
• 將 pdesolve 函數的輸出指派給函數名稱或函數向量的名稱。
• 若要變更用於偏導數的近似方法,請在 pdesolve 函數上按一下滑鼠右鍵,然後選擇其他方法。這可能會影響計算時間。
以下是使用 pdesolve 時的可能錯誤和解決方案清單。
• 錯誤:此函數需要至少 5 個引數,但僅使用 4 個。
範例:
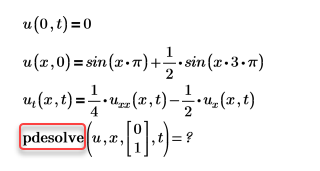
解決方案:新增缺少的引數,在本例中為 trange。
• 錯誤:此函數最多接受 7 個引數,但已使用 8 個。
範例:
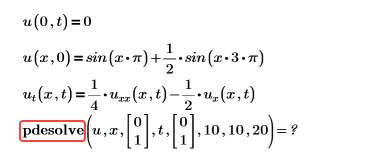
解決方案:移除不必要的引數。請參閱有關引數的詳細資訊
• 錯誤:時間變數的邊界向量異常。
範例:
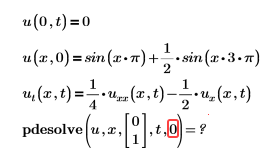
解決方案:未正確定義 trange。請參閱引數中的詳細資訊
• 錯誤:空間變數的邊界向量異常。
範例:
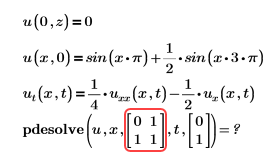
解決方案:未正確定義 xrange。請參閱引數中的詳細資訊
• 錯誤:未正確指定未知函數名稱。
範例:
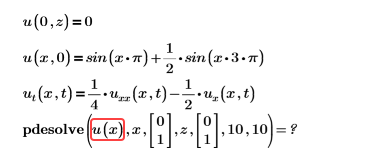
解決方案:函數必須不含引數。
• 錯誤:必須為大於 4 的整數。
範例:
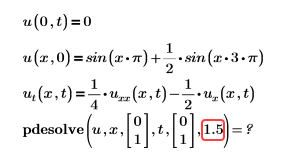
或
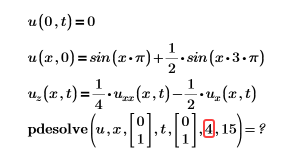
解決方案:分隔點數必須是大於 4 的整數。