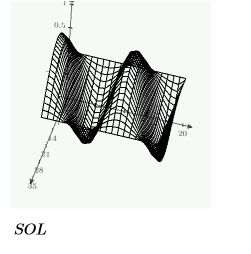
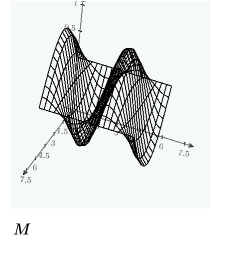
範例:解題指令群中的 PDE
在「解題指令群」中使用偏微分方程式 (PDE) 以及偏微分方程式求解器「numol」,以比較波動方程式的解。
PDE 解題指令群
求解下列一維波動方程式:
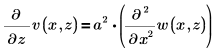
使用條件約束:
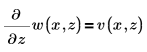
若要將第一個方程式作為兩個偏微分方程式的系統,請設定 PDE「解題指令群」
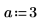
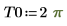
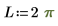
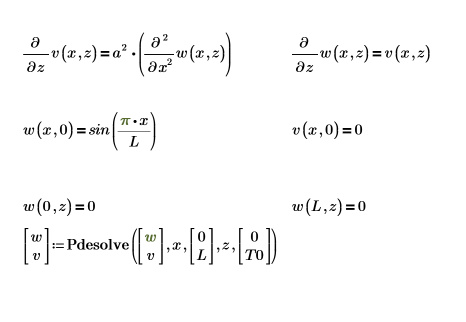
以下是邊界的單一解:
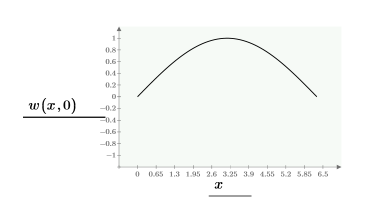
使用上述定義的條件約束,建立解的格點,以使用 CreateMesh 函數三維繪圖:
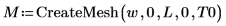
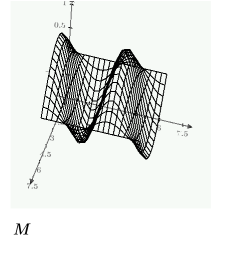
使用 numol
您可以求解指令行求解器「numol」。當您想在程式中包括計算時,這尤其有用。
定義系統中之偏微分方程式與代數條件約束的數目:
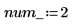
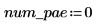
計算 PDE 右側的函數是長度 num_pde + num_pae (偏代數方程式) 的向量。在本例中,函數是方程式系統。同樣地,邊界條件定義為長度 num_pde + num_pae 的欄向量。
PDE 向量的運算式:
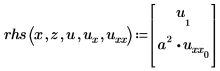
因此,如上所定義的 u1=v,以及 u0=w。
初始條件的向量:
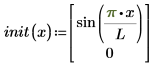
假設每個左側都是未知函數向量的第一階時間導數 u。函數的變數有 x (空間) 與 t (時間)。解可以是 u,也可以是方程式系統解的向量:ux,向量中各解 u 的第一個導數,以及 uxx,第二個空間導數。
您必須使用向量下標來處理 u、ux 及 uxx 中的個別項目。
邊界條件的向量可以有三種類型的列。每一列皆由下列其中一項決定:
• rhs 包含二階空間導數:需要兩個邊界條件 (狄里克雷「D」或紐曼「N」),積分區域的每側各一個。
• rhs 包含一階空間導數:一個狄里克雷邊界條件位於積分區域的左側或右側,另一個為「NA」。
• 若向量不含空間導數,則不需要邊界條件。
左右邊界的邊界條件會遵循下列慣例:
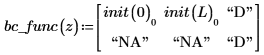
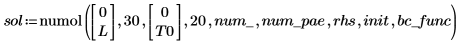
numol 的結果是一個矩陣,將空間中的每個點表示為列,並將時間中的每個點表示為欄。這可讓您一次選取一個欄,在單一時間點表示所有空間的解,因此有助於將解視覺化。求解方程式系統時,解矩陣會將每個未知函數的解矩陣附加至上一個矩陣的一側。
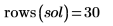
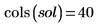
就目前範例而言,每個函數都有 20 個時間點,因此矩陣含 40 個欄。挑選第一個解 u0:
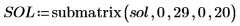
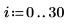
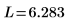
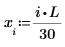
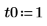
比較 numol 和 Pdesolve
在一點 t0 比較 numol 與 Pdesolve:
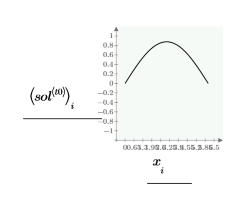
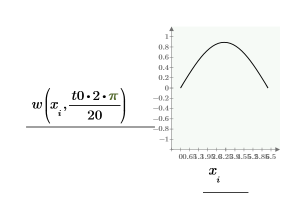
比較空間與時間值的解格點: