Аналитическое вычисление интегралов
1. Вставьте оператор интеграла.
2. Введите выражение в местозаполнитель справа от знака интеграла.
3. Введите переменную интегрирования x в местозаполнитель справа от символа d.
4. Вставьте оператор аналитического преобразования.
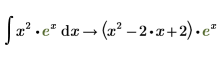
С помощью оператора аналитического преобразования можно вычислять только неопределенные интегралы. |
5. Чтобы взять определенный интеграл той же функции от 0 до 5, введите 0 в нижний местозаполнитель интеграла. Введите 5 в верхний местозаполнитель и повторите шаги 2-4.
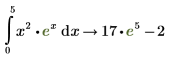
6. Чтобы взять определенный интеграл той же функции, когда хотя бы один из пределов является неопределенной переменной, повторите шаги 2-4. Затем вставьте нижний и верхний пределы интеграла.
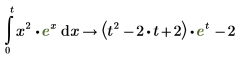
При вычислении определенного интеграла, в котором хотя бы один из пределов не определен, символьный механизм подразумевает, что верхний предел больше нижнего предела.
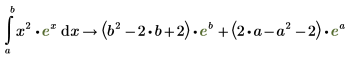
7. Чтобы назначить результаты аналитического вычисления функции, определите функцию следующим образом:
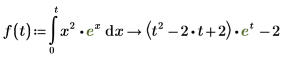
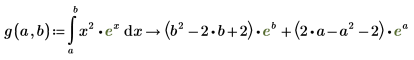
Главное значение Коши
Главное значение Коши интеграла в окрестности точки c в интервале (a,b) определяется следующим выражением:
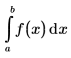
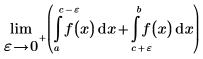
Главное значение Коши предназначается для определения значения интеграла, когда функция f имеет сингулярность в точке c. Например, следующий интеграл имеет сингулярность в точке c=0, и оператор аналитического преобразования возвращает ошибку.
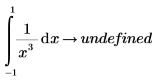
Чтобы найти главное значение Коши, необходимо добавить модификатор cauchy.
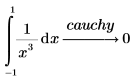
Аналитическое преобразование интегралов, для которых требуется анализ Коши, возвращает результат undefined, если не указано ключевое слово cauchy. |