Пример. Качество аппроксимации
Используйте функции polyfit и polyfitstat для выполнения линейной регрессии и дисперсионного анализа для проверки качества аппроксимации.
1. Задайте таблицу экспериментальных данных для полимерного процесса. Температура реакции t и скорость подачи катализатора fr влияют на вязкость vy полимера.

Качество аппроксимации
2. Вызовите функцию polyfit для моделирования данных с помощью линейной регрессии.
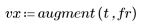
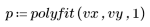
3. Вычислите прогнозируемую вязкость для всех параметров температуры и скорости подачи.
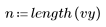
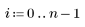
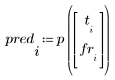
4. Вычислите невязки (разность между моделируемыми и измеренными значениями).
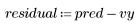
5. Постройте графики зависимости невязок от наблюдаемой вязкости, температуры и скорости подачи.
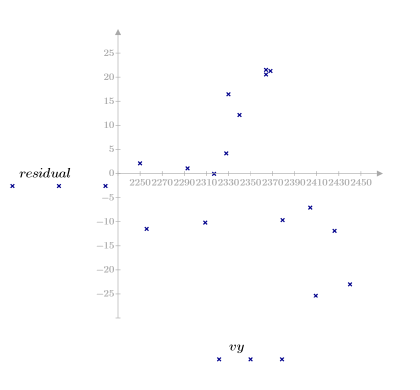
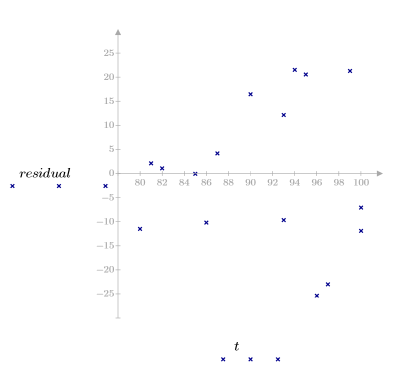
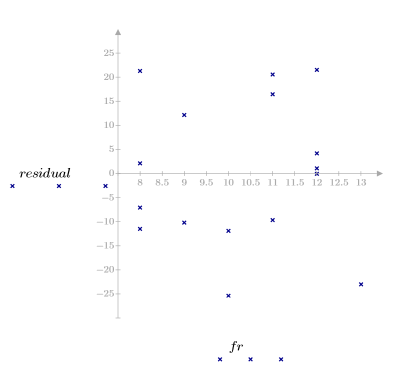
Графики невязки указывают на то, что дисперсии наблюдаемой вязкости и температуры растут с увеличением вязкости и температуры соответственно.
6. Вызовите функцию polyfitstat для расчета различных статистических показателей для линейной модели. Отобразите матрицу ANOVA, возвращаемую функцией polyfitstat в строке 8.
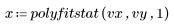
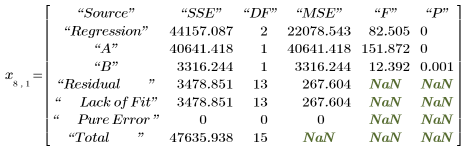
В матрице ANOVA источники дисперсии разделены между регрессией и компонентами невязки. Компонент регрессии дополнительно разделен между коэффициентами регрессии. Однако невозможно различить отсутствие согласия и истинные ошибки для невязок, поскольку экспериментальные значения vy не имеют реплик.
Вычисление таблицы ANOVA и ее использование для регрессии
1. Вычислите сумму вследствие ошибки (SSE).
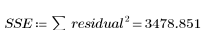
SSE равно χ2 (общий показатель согласия). Это значение минимизируется при поиске решения методом наименьших квадратов. Ошибка представляет собой критерий соответствия модели данным. Она является той величиной отклонения, которую нельзя объяснить регрессией.
2. Задайте число степеней свободы для ошибки df_error с учетом общего числа степеней свободы df_total и числа степеней свободы для параметров df_param. Число степеней свободы равно размерности данных за вычетом числа параметров аппроксимации.
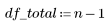
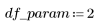
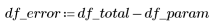
3. Определите сумму квадратов вследствие регрессии (SSR) относительно общей суммы квадратов (SST).
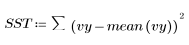
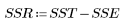
4. Определите среднеквадратическую ошибку (MSE) и среднеквадратическую регрессию (MSR). Разделите ошибку на соответствующее число степеней свободы.
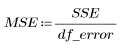
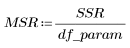
5. Составьте таблицу дисперсионного анализа для описания аппроксимации.
Сумма квадратов | DF | Среднеквадратичные значения | F-фактор | |
|---|---|---|---|---|
Регрессия | 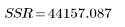 | 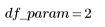 | 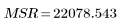 | 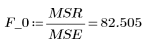 |
Ошибка | 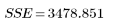 | 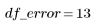 | 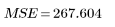 | |
Total | 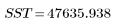 | 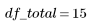 |
Эту таблицу можно сравнить с матрицей ANOVA функции polyfitstat.
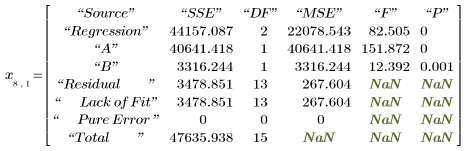
6. Оцените качество согласия модели с данными:
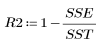
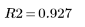
Это показатель того, что 92.7 % изменчивости вязкости может быть объяснено моделью линейной регрессии.
7. Задайте уровень значимости для критерия проверки гипотезы, чтобы убедиться в том, что модель соответствует данным.
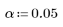
8. Вычислите критическое значение F.
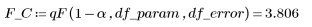
9. Проверьте гипотезу о том, что модель соответствует данным.
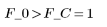
Примите гипотезу. С помощью этой линейной модели можно прогнозировать вязкость полимера.
Справочная информация
Montgomery, D.C., Design and Analysis of Experiments, 5th ed., John Wiley & Sons, New York, 2001, стр. 398