Пример. Выявление значимых наблюдений
Используйте функцию polyfitstat, чтобы проверить наблюдения, используемые для создания многомерной полиномиальной регрессии.
1. Задайте матрицу, которая содержит замеры, взятые у 20 здоровых людей возрастом от 25 до 34 лет.
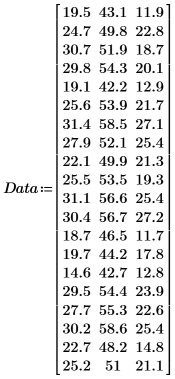
Столбцы матрицы представляют толщину кожной складки на трицепсе, окружность бедра и жировую складку, соответственно, для каждого из этих 20 человек.
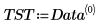
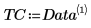
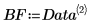
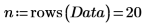
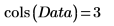
3. Используйте функцию augment, чтобы определить матрицу BM как первые два столбца матрицы. Эти измерения можно использовать, чтобы предсказать количество жира в организме человека.
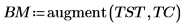
4. Вызовите функцию polyfitstat, чтобы смоделировать эксперимент с помощью регрессии первого порядка и рассчитать статистику регрессии.
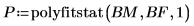
5. Отобразите матрицу коэффициентов регрессии, находящуюся в строке 7 выходной матрицы P.
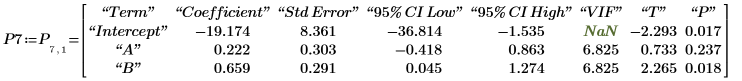
6. Вычислите коэффициенты регрессии с использованием матричных вычислений.
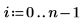
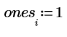
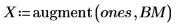
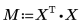
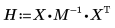
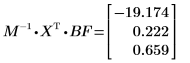
Коэффициенты регрессии соответствуют следующему уравнению:
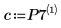
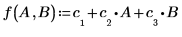
7. Используйте уравнение регрессии для расчета прогнозируемого количества телесного жира. Сравните эти значения с количеством телесного жира, полученным в результате измерений.
 |  |
8. Используйте функцию submatrix, чтобы отображать статистические данные модели, найденные в первых строках выходной матрицы P.

Первая статистика представляет среднеквадратическое отклонение для регрессии.
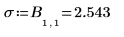
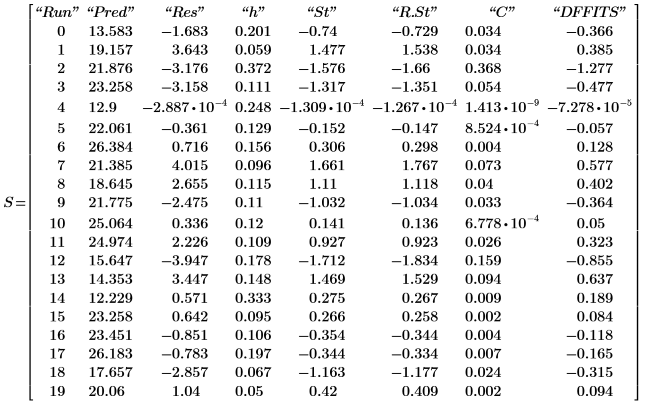
9. Отобразите диагностику модели, которую можно найти в последней вложенной матрице выходной матрицы P.
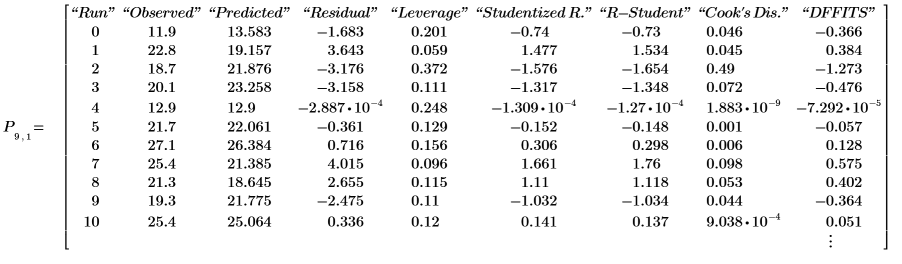
Фактическое и прогнозируемое значения соответствуют значениям, показанным на шаге 7. Остатки представляют собой разницу между фактическими и прогнозируемыми значениями:
10. Рассчитайте остатки, т. е. разницу между фактическими и прогнозируемыми значениями.
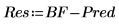
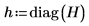
12. Вычислите стьюдентизированные остатки.
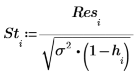
Ниже рассчитаны внешне стьюдентизированные остатки, или R-стьюдент. Константа p представляет количество коэффициентов, рассчитанных для регрессии, а S2 является ожидаемой величиной s2 для набора данных, из которого удалено наблюдение номер i.
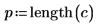
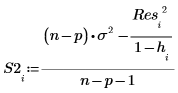
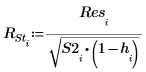
13. Используйте расстояние Кука, чтобы измерить полное влияние удаленной точки на линейную регрессию.
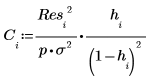
14. Вычислите разницу между прогнозируемыми значениями, когда все наблюдения включены в значения приближения, и прогнозируемые значения, когда опущено i-е наблюдение
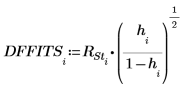

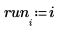
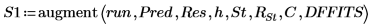
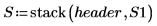
16. Используйте функции max и qt, чтобы определить наибольшее значение R-стьюдента в наборе данных. Используйте критерий Бонферрони, чтобы решить, является ли соответствующее наблюдение отклонением.
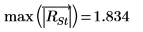
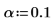
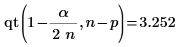
Наибольшее значение R-стьюдента меньше критерия Бонферрони, что указывает на то, что соответствующее наблюдение не является отклонением.
17. Определите максимальное значение DFFITS.
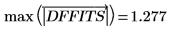
Значение больше 1, но достаточно близко к 1, что указывает на то, что соответствующее наблюдение не обязательно является существенным.
18. Постройте график влияния индексов, располагая значения расстояния Кука напротив интервалов.
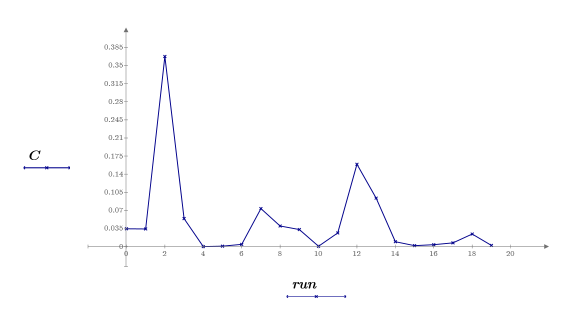
Наблюдение для run2 является наиболее существенным наблюдением в наборе данных. Наблюдение для run12, определяемое на шаге 10, также является существенным, но в меньшей степени, чем для run2.
Справочная информация
Источник: Neter, J., Kutner, M.H., Nachtsheim, C.J., Wasserman, W., Applied Linear Statistical Models (Прикладные линейные статистические модели), 4th ed., McGraw-Hill/Irwin, Boston, 1996, стр. 375