Пример. Решатель пространства состояний
Используйте решатель statespace, чтобы решить представление пространства состояний системы обыкновенных дифференциальных уравнений (ОДУ) первого порядка.
А именно, найдите решение для случая свободного гармонического осциллятора, для которого правая часть уравнения гармонических колебаний равняется 0:
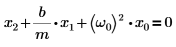
Есть четыре случая решения: сильное затухание, критическое затухание, слабое затухание и полная обратная связь по состоянию. |
Решение для сильного затухания
1. Запишите математическое уравнение для случая сильного затухания:
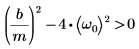
2. Определите начальные условия, массу объекта, константу затухания, начало и конец интервала интегрирования и число точек:
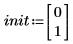
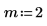
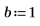
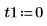
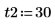
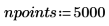
3. Задайте естественную, или резонансную, частоту системы.
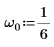
4. Проверьте, что существует условие сильного затухания:
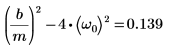
5. Запишите ОДУ в матричной форме:
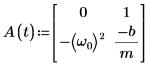
6. Вызовите функцию statespace:
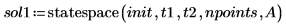
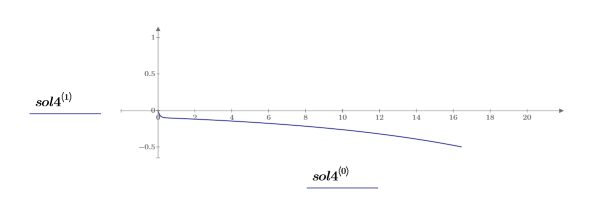
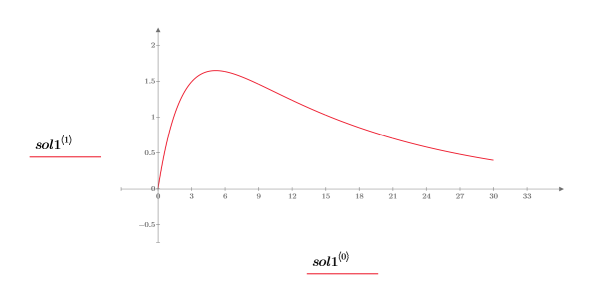
7. Постройте график решения:
Решение для критического затухания
1. Задайте естественную, или резонансную, частоту системы.
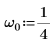
2. Проверьте, что существует условие критического затухания:
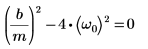
3. Запишите ОДУ в матричной форме:
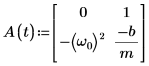
4. Вызовите функцию statespace:
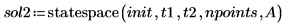
5. Постройте график решения:
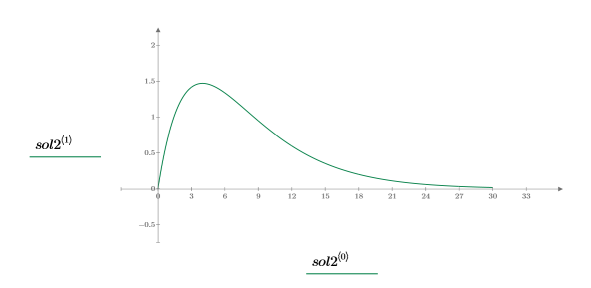
Решение для слабого затухания
1. Задайте естественную, или резонансную, частоту системы.
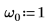
2. Проверьте, что существует условие слабого затухания
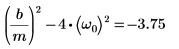
3. Запишите ОДУ в матричной форме:
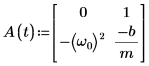
4. Вызовите функцию statespace:
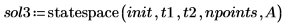
5. Постройте график решения:
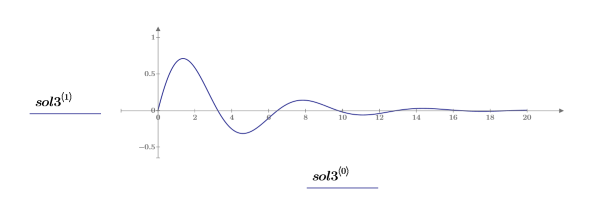
Решение для полной обратной связи по состоянию
1. Задайте начальные условия.
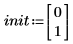
2. Запишите ОДУ в матричной форме.
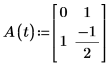
3. Определите дополнительные функции.
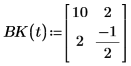
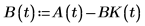
4. Вызовите функцию statespace.
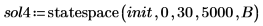
5. Постройте график решения.