Metodo di rilassamento per un'equazione differenziale alle derivate parziali
• relax(A, B, C, D, E, S, U, rjac)
• multigrid(M, ncycle)
Restituiscono una matrice quadrata in cui la posizione di un elemento nella matrice corrisponde alla sua posizione in una regione quadrata in cui tale elemento assume un valore che approssima la soluzione dell'equazione differenziale alle derivate parziali di Poisson
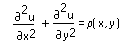
in tale punto. La funzione relax risolve l'equazione di Poisson utilizzando il metodo di Gauss-Seidel modificato con un sovrarilassamento successivo sulla griglia.
La funzione multigrid calcola la soluzione per il caso speciale in cui tutte le condizioni limite in U sono uguali a zero, utilizzando il metodo multigrid.
• Se le condizioni limite sono costanti e uguali su tutti e quattro i lati, trasformare l'equazione in modo da ottenere condizioni limite uguali a zero su tutti i lati e utilizzare multigrid, che è più facile e veloce da configurare.
• Se ρ = 0, l'equazione di Poisson si riduce all'equazione di Laplace.
• Per risolvere un'equazione differenziale alle derivate parziali iperbolica o parabolica, oppure un sistema di equazioni differenziali alle derivate parziali, utilizzare numol.
Argomenti
• A, B, C, D, E sono matrici quadrate reali con le stesse dimensioni, che contengono i coefficienti dell'approssimazione di Laplace discretizzata della funzione u in corrispondenza dei quattro vicini più prossimi e del punto di approssimazione.
• S è una matrice quadrata che contiene il termine di origine corrispondente a ogni punto all'interno del quadrato.
• U è una matrice quadrata che contiene i valori al limite lungo i bordi della regione e i valori ipotizzati iniziali per la soluzione all'interno della regione.
• rjac è un valore reale 0 < rjac < 1, utilizzato per indicare il raggio spettrale dell'iterazione di Jacobi. che consente di controllare la convergenza dell'algoritmo di rilassamento.
Il valore ottimale di rjac dipende dai dettagli del problema, tuttavia come valore iniziale è possibile utilizzare r, dove n è il numero di punti sulla griglia in ogni direzione.
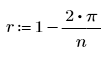
• M è una matrice quadrata con dimensioni uguali a 1 + 2n, i cui elementi contengono il termine di origine nel punto corrispondente del dominio quadrato.
• ncycle è il numero intero di cicli a ogni livello dell'iterazione eseguita da multigrid.
Specificando 2 come valore di ncycle si ottiene in genere una buona approssimazione della soluzione.