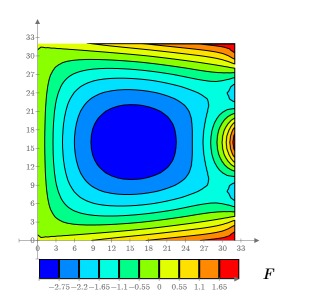
Esempio: flusso di calore su una piastra quadrata

Funzioni > Soluzione e ottimizzazione > Solutori di equazioni differenziali > Esempio: flusso di calore su una piastra quadrata - II

Esempio: flusso di calore su una piastra quadrata - II

Risolvere la distribuzione di temperatura stazionaria di una piastra quadrata utilizzando il solutore di equazioni differenziali parziali relax.

Risoluzione di un'equazione di Poisson

Risolvere l'equazione del calore in cui i valori della funzione di origine sono noti e le condizioni limite sono diverse da zero.

La funzione relax è basata su un metodo di risoluzione completamente diverso e pertanto richiede un insieme diverso di argomenti.

1. Definire cinque matrici quadrate a, b, c, d e e perché contengano i coefficienti per l'approssimazione di Laplace:

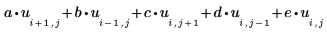
Questi array possono essere di qualsiasi dimensione specificata. Più grandi sono gli array, più precisa sarà la mesh nella soluzione.

2. Definire la dimensione della piastra quadrata:

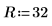
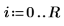
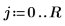
3. Definire i coefficienti:

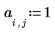
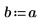
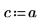
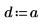
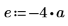
4. Definire l'intensità e la posizione di una fonte costante.

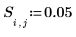
5. Definire una matrice quadrata f, con dimensioni uguali alla griglia, perché contenga i valori limite noti della funzione F(x,y) e i valori ipotizzati per i valori interni sconosciuti.

◦ Condizione limite lungo la parte superiore:

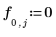
◦ Condizione limite lungo la parte inferiore:

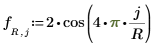
◦ Condizione limite lungo i bordi:

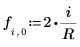
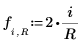
6. Definire la variabile Jacobi spectral radius r, in modo che sia un numero reale compreso tra 0 e 1.

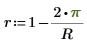
Questo parametro controlla la convergenza dell'algoritmo. Se viene visualizzato il messaggio di errore indicante un numero eccessivo di iterazioni, provare a ridurre r.

7. Chiamare la funzione relax:

<region id="ID0E2O15" top="1516.8000000000002" left="38.400000000000006" height="25.6" width="204.10333333333335" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="30">
    <define xmlns="http://schemas.mathsoft.com/math50">
      <id xml:space="preserve" labels="VARIABLE">F</id>
      <apply>
        <id xml:space="preserve" labels="FUNCTION" label-is-contextual="true">relax</id>
        <sequence>
          <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true">a</id>
          <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true">b</id>
          <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true">c</id>
          <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true">d</id>
          <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true">e</id>
          <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true">S</id>
          <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true">f</id>
          <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true">r</id>
        </sequence>
      </apply>
    </define>
  </math>
</region>

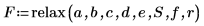
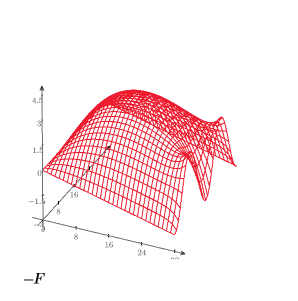
8. Creare un grafico 3D per mostrare la distribuzione del calore sulla piastra quadrata.

Fare clic per copiare questa espressione

<region id="ID0ELQ15" top="1747.2000000000003" left="38.400000000000006" height="301.40000715255735" width="297.6000071525574" xmlns="http://schemas.mathsoft.com/worksheet50">
  <plot background-type="white">
    <plot3D>
      <traces>
        <trace3D resultRef="32" num-of-points="41" SurfaceFill="#00FFFFFF">
          <traceStyle color="#FFED1D2F">surface</traceStyle>
        </trace3D>
      </traces>
      <graph-size width="240.00000715255737" height="240.00000715255737" />
      <axes>
        <xAxis rank="1" start="0" end="32">
          <axisLine />
          <axisGrid>
            <gridFrequency>5</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <numberFormat>
            <general precision="3" />
          </numberFormat>
          <xyDomain auto-scale="true" allow-negative-values="true" scale-type="linear">
            <startValue />
            <endValue />
          </xyDomain>
        </xAxis>
        <yAxis rank="1" start="0" end="32">
          <axisLine />
          <axisGrid>
            <gridFrequency>5</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <numberFormat>
            <general precision="3" />
          </numberFormat>
          <xyDomain auto-scale="true" allow-negative-values="true" scale-type="linear">
            <startValue />
            <endValue />
          </xyDomain>
        </yAxis>
        <zAxis rank="1" start="-3" end="4.5">
          <axisLine />
          <axisGrid>
            <gridFrequency>6</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <numberFormat>
            <general precision="3" />
          </numberFormat>
          <zDomain auto-scale="true" allow-negative-values="true" scale-type="linear">
            <startValue />
            <endValue />
          </zDomain>
        </zAxis>
      </axes>
      <plotEquations>
        <plotEquation>
          <math>
            <apply xmlns="http://schemas.mathsoft.com/math50">
              <neg />
              <id xml:space="preserve">F</id>
            </apply>
          </math>
          <math>
            <placeholder xmlns="http://schemas.mathsoft.com/math50" />
          </math>
        </plotEquation>
      </plotEquations>
      <CameraTransformMatrix Columns="4" Rows="4">
        <Cells>
          <Cell>-0.052623873051966662</Cell>
          <Cell>0.043294250885890617</Cell>
          <Cell>0.99767546618388891</Cell>
          <Cell>0</Cell>
          <Cell>0.095704097834471175</Cell>
          <Cell>0.99467978821191028</Cell>
          <Cell>-0.038116198399097093</Cell>
          <Cell>0</Cell>
          <Cell>-0.99401783366431629</Cell>
          <Cell>0.093475808436936883</Cell>
          <Cell>-0.056487340124674094</Cell>
          <Cell>0</Cell>
          <Cell>0</Cell>
          <Cell>0</Cell>
          <Cell>0</Cell>
          <Cell>1</Cell>
        </Cells>
      </CameraTransformMatrix>
      <CameraType>Orthographic</CameraType>
    </plot3D>
  </plot>
</region>

9. Creare un grafico a curve di livello per mostrare le linee di temperatura costante.

Argomenti correlati

Metodo di rilassamento per un'equazione differenziale alle derivate parziali

È stato utile?