Solutori di equazioni differenziali
I solutori di equazioni differenziali ordinarie (ODE, Ordinary Differential Equation) consentono di risolvere un'equazione o un sistema di equazioni per funzioni incognite di una variabile. I solutori di equazioni differenziali parziali (PDE, Partial Differential Equation) trovano la soluzione per funzioni di due variabili (PDE 1D).
Equazioni differenziali ordinarie
Per risolvere un'equazione ODE direttamente, senza creare un blocco di soluzione, utilizzare uno dei solutori ODE, che risolvono sistemi di equazioni ODE con la forma indicata di seguito.
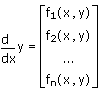
dove y è un vettore di funzioni incognite della variabile indipendente x. Per risolvere un'equazione ODE di ordine superiore, riscriverla come sistema di equazioni ODE del primo ordine.
I solutori di equazioni ODE possono essere di due tipi, ovvero solutori per sistemi stiff e solutori per sistemi non stiff. Un sistema di equazioni ODE in forma matriciale, ad esempio y’=Ay, è denominato stiff se la matrice A è quasi singolare. In caso contrario, il sistema è detto non stiff.
• Adams - Metodi di Adams-Bashford.
• rkfixed, Rkadapt, Bulstoer - Metodo di Runge Kutta di ordine 4, con dimensione di passo fissa e adattiva e metodo di Bulstoer per ODE con variazioni regolari.
• BDF - Metodi con formule di differenziazione a ritroso.
• Radau, Stiffb, Stiffr - Metodi RADAU, Bulirsch-Stoer e Rosenbrock per sistemi di tipo stiff.
• AdamsBDF - Determina se un sistema è di tipo stiff o non stiff e, a seconda del caso, richiama BDF o Adams.
• statespace - Sistemi di equazioni differenziali ordinarie lineari del primo ordine.
• bvalfit, sbval - Problemi con valore limite, in cui non tutte le condizioni iniziali sono note, convertiti in problemi ai valori iniziali mediante metodo di shooting lineare.
Esiste inoltre un'ampia gamma di generatori di polinomi speciali e funzioni ipergeometriche per la soluzione di specifiche equazioni ODE comuni.
Equazioni differenziali parziali
• numol - Solutore da riga di comando per sistemi iperbolici e parabolici di PDE 1D, comprese equazioni differenziali ordinarie accoppiate e vincoli algebrici.
• relax, multigrid - Solutori da riga di comando per PDE ellittiche di Poisson/Laplace.
I solutori numol e multigrid non sono intercambiabili, perché gestiscono dimensioni fisiche e spaziali diverse.
• numol è progettato per la soluzione di equazioni PDE 1D iperboliche e paraboliche dipendenti dal tempo (funzioni di x,t).
• multigrid è progettato per la soluzione di equazioni PDE 2D ellittiche stazionarie (funzioni di x,y) in un intervallo quadrato.
Calcolo dello jacobiano
• Jacob - Restituisce la matrice jacobiana di un vettore.