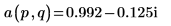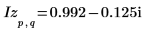Esempio: dft e idft di una matrice
Utilizzare le funzioni dft e idft per trovare la trasformata discreta diretta o inversa di Fourier di una matrice.
1. Definire le dimensioni di una matrice di dati.
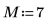
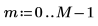
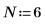
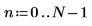
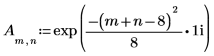
3. Utilizzare la funzione dft per calcolare la trasformata discreta di Fourier di A.
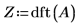
4. Utilizzare la definizione di dft per calcolare un elemento specifico di Z.
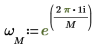
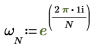
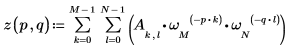
5. Utilizzare la definizione precedente per trovare un elemento di frequenza specifico e confrontarlo con l'output della funzione dft.
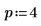
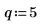
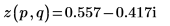
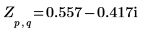
Funzione idft gaussiana
La funzione idft è la trasformazione inversa di dft. Accetta come argomento una matrice reale o complessa e restituisce una matrice delle stesse dimensioni.
1. Mostrare che la trasformazione inversa di una funzione dft è la funzione stessa.
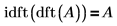
2. Utilizzare la matrice definita in precedenza A, quindi mostrare che la trasformazione inversa di una funzione dft è la funzione stessa.
 |  |
3. Utilizzare la definizione di idft per calcolare qualsiasi elemento di A.
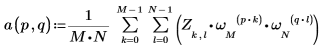
4. Utilizzare la definizione precedente per trovare un elemento di frequenza specifico e confrontarlo con l'elemento corrispondente nell'output della funzione idft.