Esempio: DFT di funzioni complesse
Utilizzare le funzioni dft e idft per calcolare la trasformata di Fourier complessa o reale oppure la trasformata diretta o inversa di Fourier.
1. Creare alcuni dati complessi simulati con N punti dati.
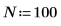
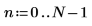
2. Definire la spaziatura di campionamento.
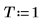
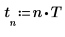
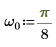
3. Utilizzare la funzione exp per definire il segnale seguente.
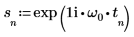
4. Definire la frequenza di campionamento e la frequenza corrispondente al n-esimo elemento nel vettore trasformato.
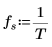
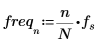
5. Applicare la funzione dft per trasformare i dati nel dominio delle frequenze.
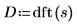
6. Salvare la grandezza degli elementi dell'array D in un nuovo array.
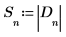
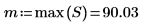
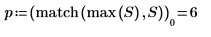
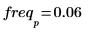
8. Tracciare il grafico della grandezza di DFT come funzione della frequenza.
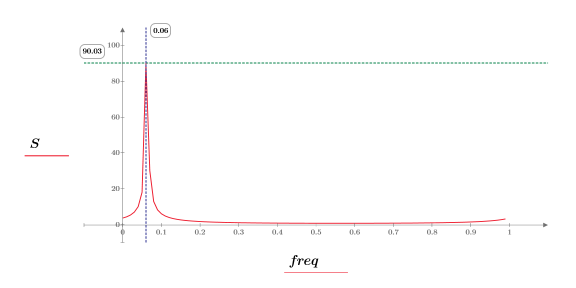
9. Mostrare che la frequenza del picco corrisponde a ω0/2π.
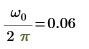
10. Utilizzare la funzione idft per mostrare che la funzione IDFT di DFT di un segnale restituisce il segnale stesso.