Trasformata discreta di Fourier di dati
• dft(A), idft(Z) - Restituiscono la trasformata diretta/inversa di Fourier di un vettore o di una matrice con valori complessi.
Se l'input dft è un vettore V di lunghezza r:
◦ L'output di dft(V) è un vettore Z di lunghezza r.
◦ L'output di idft(Z) è un vettore di lunghezza r.
Se l'input di dft è una matrice M di righe r e colonne c:
◦ L'output di dft(M) è una matrice P di righe r e colonne c.
◦ L'output di idft(P) è una matrice di righe r e colonne c.
• dftr(B), idftr(Z) - Restituiscono la trasformata diretta/inversa di Fourier di un vettore o di una matrice con valori reali.
Se l'input dftr è un vettore V di lunghezza r:
◦ L'output di dftr(V) è un vettore Z di lunghezza L, dove L=floor(r/2)+1. Gli elementi di Z sono identici ai primi elementi L dell'output di dft(V).
◦ L'output di idftr(Z) è un vettore di lunghezza r=2(L-1).
Se l'input di dftr è una matrice M con righe r e colonne c:
◦ L'output di dftr(M) è una matrice P con righe r e colonne L, dove L=floor(c/2)+1. Gli elementi di P sono identici alle prime colonne L dell'output di dft(M).
◦ L'output di idftr(P) è una matrice di righe r e colonne c=2(L-1).
Argomenti
• A è una matrice o un vettore di qualunque dimensione con valori complessi.
• B è una matrice o un vettore con valori reali. Eventuali parti immaginarie vengono ignorate. Se B è un vettore, il numero di righe deve essere un multiplo di 2. Se B è una matrice, il numero di colonne deve essere un multiplo di 2.
• I dati devono avere unità compatibili sia per A che per B.
Trasformata di Fourier di vettori
• Se A è un vettore di dimensione m, l'elemento u-esimo della trasformata diretta monodimensionale (1D) del vettore A è dato da Zu, come illustrato di seguito.
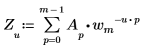
Dove:
◦ m è il numero di righe e l'elemento u è definito come: 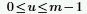
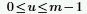
◦ i è l'unità immaginaria e l'elemento wm è definito come:
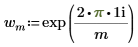
La valutazione di Z nella definizione precedente equivale all'applicazione della funzione dft al vettore A.
• Se Z è un vettore di dimensione m, l'elemento u-esimo della trasformata inversa monodimensionale (1D) del vettore Z è dato da Au, come illustrato di seguito.
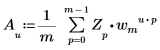
Dove:
◦ gli elementi m, u e wm sono definiti in precedenza.
La valutazione di A nella definizione precedente equivale all'applicazione della funzione idft al vettore Z.
Trasformata di Fourier di matrici
• Se A è una matrice di dimensione mxn, l'elemento (u,v)-esimo della trasformata diretta bidimensionale (2D) della matrice A è dato da Zu,v, come illustrato di seguito.
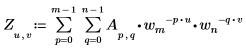
Dove:
◦ gli elementi m, u e wm sono definiti in precedenza.
◦ n è il numero di colonne e l'elemento v è definito come: 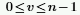
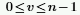
◦ i è l'unità immaginaria e l'elemento wn è definito come:
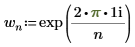
La valutazione di Z nella definizione precedente equivale all'applicazione della funzione dft alla matrice A.
• Se Z è una matrice di dimensione mxn, l'elemento (u,v)-esimo della trasformata inversa bidimensionale (2D) della matrice A è dato da Au,v, come illustrato di seguito.
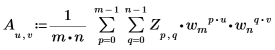
Dove:
◦ gli elementi m, n, u, v, wm e wn sono definiti in precedenza.
La valutazione di A nella definizione precedente equivale all'applicazione della funzione idft alla matrice Z.
Ulteriori informazioni
• L'esecuzione delle funzioni di Fourier risulta più rapida quando il numero delle righe di un vettore e delle colonne di una matrice è una potenza di 2.
• Le nuove funzioni dft/idft sostituiscono le funzionalità delle funzioni obsolete cfft/icfft e CFFT/ICFFT e offrono prestazioni migliorate soprattutto per insiemi di dati più grandi e casi in cui la dimensione non è una potenza di 2.
• Le nuovi funzioni dftr/idftr sostituiscono le funzionalità delle funzioni obsolete fft/ifft e FFT/IFFT.
La funzione dftr è utilizzabile su vettori reali la cui lunghezza è un numero pari e su matrici con un numero pari di colonne.
• Le funzioni fft/FFT sono utilizzabili solo su vettori reali la cui lunghezza è una potenza di 2.
• Le funzioni ifft/IFFT hanno una lunghezza pari solo alla metà di quella del vettore di input più uno oppure a 2k-1+1 in cui k è un numero intero > 1. L'altra metà, che è il coniugato della prima parte con l'ordine invertito, deve essere ricostruita manualmente. Le funzioni dft/idft restituiscono il risultato completo.
• Le funzioni dft/idft differiscono dalle funzioni fft/ifft, FFT/IFFT e cfft/icfft, CFFT/ICFFT obsolete sia per il fattore di scala che per il segno dell'esponente.
◦ Le differenze per le trasformate dirette sono illustrate di seguito.
dft/dftr | fft/cfft | FFT/CFFT | |
|---|---|---|---|
Fattore di scala | 1 | 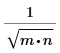 | 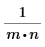 |
Segno dell'esponente | Negativo | Positivo | Negativo |
◦ Le differenze per le trasformate inverse sono illustrate di seguito.
idft/idftr | ifft/icfft | IFFT/ICFFT | |
|---|---|---|---|
Fattore di scala | 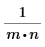 | 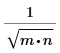 | 1 |
Segno dell'esponente | Positivo | Negativo | Positivo |
Quando si calcola il fattore di scala per le funzioni che operano solo su vettori (casi 1D), presupporre che n=1.