• Ognuna delle funzioni riportate di seguito restituisce una matrice di soluzione (intvls+1)×(n+1), dove n è il numero di incognite. La prima colonna della matrice contiene i valori di x per cui vengono valutate le soluzioni. Tali valori sono numeri (intvls + 1) distanziati uniformemente, compresi tra x1 e x2. Le colonne restanti contengono i valori delle soluzioni y0,y1,...,yn-1 corrispondenti ai valori di x nella prima colonna.

• Per i risolutori rkfixed, RkAdapt, Bulstoer, Stiffb e Stiffr è possibile specificare una tolleranza scalare per la soluzione definendo la variabile TOL prima di chiamare il risolutore. Ad esempio, è possibile impostare 10-6 come tolleranza per tutte le variabili.

• Per semplificare l'immissione delle equazioni e delle condizioni iniziali, è possibile utilizzare blocchi di soluzione ODE.

• Adams(init, x1, x2, intvls, D, [tol]) - Utilizza i metodi di Adams.

• rkfixed(init, x1, x2, intvls, D) - Utilizza il metodo a passo fisso di Runge-Kutta del quarto ordine.

• Rkadapt(init, x1, x2, intvls, D) - Utilizza il metodo Runge-Kutta del quarto ordine con dimensione del passo adattiva.

• Bulstoer(init, x1, x2, intvls, D) - Utilizza il metodo di Bulirsch-Stoer, che è leggermente più accurato del metodo di Runge-Kutta, ma richiede un sistema con variazioni regolari.

• BDF(init, x1, x2, intvls, D, [J], [tol]) - Utilizza metodi con formule di differenziazione a ritroso. È possibile utilizzare uno qualsiasi degli argomenti facoltativi J o tol e omettere l'altro.

• Radau(init, x1, x2, intvls, D, [J], [M], [tol]) - Utilizza il metodo Radau5. È possibile utilizzare qualsiasi combinazione degli argomenti facoltativi J, M e tol e omettere le opzioni che non si desidera utilizzare.

• Stiffb(init, x1, x2, intvls, D, AJ) - Utilizza il metodo di Bulirsch-Stoer.

• Stiffr(init, x1, x2, intvls, D, AJ) - Utilizza il metodo di Rosenbrock.

• AdamsBDF(init, x1, x2, intvls, D, [J], [tol]) - Determina se un sistema è di tipo stiff o non stiff e, a seconda del caso richiama Adams o BDF. È possibile utilizzare uno qualsiasi degli argomenti facoltativi J o tol e omettere l'altro.

• init è un vettore di n valori iniziali reali (dove n è il numero di incognite) o un singolo valore iniziale scalare, nel caso di una singola ODE.

• x1 e x2 sono i punti finali scalari reali dell'intervallo su cui viene valutata la soluzione delle ODE. I valori iniziali in init sono i valori delle funzioni ODE valutate in x1

• intvls è il numero intero di intervalli di discretizzazione utilizzati per interpolare la funzione di soluzione. Il numero dei punti di soluzione è il numero di intervalli + 1.

• D è una funzione vettoriale di tipo D(x,y) che specifica il lato destro del sistema.

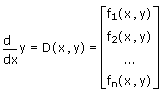
• tol (facoltativo) è un valore reale o un vettore di valori reali che specifica le tolleranze per ogni variabile indipendente nel sistema. La tolleranza è la precisione richiesta per una variabile della soluzione.

◦ È necessario impostare tol su un valore minore o uguale a 10-5. In funzione della scala del problema e della dimensione di passo utilizzata, per ottenere le soluzioni appropriate può essere necessario ridurre il valore di TOL. Minore è il valore di tol, maggiore è il numero dei passi eseguiti dall'algoritmo del risolutore per ottenere la precisione richiesta.

◦ Se si sta risolvendo un sistema di equazioni, impostando tol su uno scalare si specifica la stessa tolleranza per tutte le variabili del sistema. Impostando tol su un vettore con lunghezza uguale al numero di variabili del sistema, si specificano tolleranze diverse per le singole variabili.

• J (facoltativo) è una funzione di tipo J(x, y) che restituisce la matrice jacobiana, ovvero la matrice delle derivate parziali delle funzioni contenute in D rispetto a y0, y1, ... yn−1.

• M (facoltativo) è una matrice reale che rappresenta una combinazione qualsiasi di due variabili, nella forma M · dy/dt = f(t, y).

• AJ è una funzione di tipo AJ(x, y) che restituisce la matrice jacobiana aumentata, in cui la prima colonna contiene le derivate parziali, rispetto a x, delle funzioni del lato destro del sistema. Le colonne restanti sono le colonne della jacobiana J, che contengono le derivate parziali rispetto a y0,y1, ... yn−1.

• Le funzioni di Radau e Rkadapt utilizzano internamente dimensioni passo non uniformi quando risolvono l'equazione differenziale, aggiungendo ulteriori passi nelle regioni in cui la soluzione varia maggiormente, ma restituiscono la soluzione per il numero di punti distribuiti uniformemente specificati in intvls.

• La funzione Radau non richiede una matrice jacobiana in input, anche se l'argomento J può essere ottenuto rapidamente. L'utilizzo di tale argomento consente di aumentare la precisione.