Estadísticas de regresión polinomial multivariada
• polyfitstat(X, Y, n/"terms"/M, [conf]): Permite devolver datos estadísticos de un modelo de regresión polinomial que se ajusta a los resultados registrados en la matriz Y a los datos encontrados en la matriz X. La ecuación de regresión polinomial se puede definir de acuerdo con su orden polinomial n o con sus términos según se han especificado en la cadena “terms” o en la matriz M. Utilice la matriz M si no desea incluir la intercept en el ajuste polinomial. Utilice el argumento opcional conf para especificar un intervalo de confianza distinto del intervalo por defecto, que es del 95 %.
La segunda columna de la matriz que devuelve polyfitstat contiene los siguientes elementos:
|
Fila
|
Descripción
|
|---|---|
|
1
|
La desviación estándar para Y
|
|
2, 3, 4
|
R2, R2 ajustado y R2 previsto
|
|
5
|
PRESS: suma de cuadrados del error de predicción (útil para el escalado de valores residuales)
|
|
6
|
Estadística de prueba de Durbin-Watson para autocorrelación
|
|
7
|
Matriz de coeficientes de regresión devuelta por polyfitc
|
|
8
|
Matriz de análisis de varianza (ANOVA) para el modelo de regresión con columnas idénticas a la tabla de resultados devuelta por anova y con las siguientes filas:
• Regresión: subtotal, que después se desglosa para cada término (excepto el término intercepto)
• Residual (error): subtotal, que después se desglosa entre el error de falta de ajuste y el error de experimental puro
• Total del modelo de regresión
|
|
9
|
Matriz de diagnósticos con las siguientes columnas:
1. Numeración para cada ejecución o punto de datos
2. Resultado observado para cada ejecución o punto de datos
3. Resultado previsto por el modelo de regresión que se está investigando
4. Residual: diferencia entre el resultado observado y el resultado previsto
5. Equilibrado: medida de la distancia entre el resultado observado y el punto situado en el centro de todos los resultados observados
6. Residual estudentizado: valor residual dividido por la varianza según el resultado observado
7. R de Student: valor residual dividido por la varianza según un conjunto de datos del que se ha quitado el resultado observado
8. Distancia de Cook: medida de la influencia del resultado observado sobre todos los demás puntos de datos
9. DFFITS: diferencia entre el resultado previsto por un modelo de regresión según un conjunto de datos en el que se incluyen el resultado observado y el resultado previsto por otro modelo del que se ha quitado el resultado observado
|
Argumentos
• X es una matriz de diseño o una matriz en la que cada columna representa una variable independiente. Cada columna de X debe tener unidades compatibles.
• Y es un vector o una matriz de resultados medidos o simulados en que cada fila contiene el resultado de cada ejecución o el punto de datos definido en X. Si las filas no contienen el mismo número de réplicas, rellene los elementos vacíos de Y en NaN. Los elementos de Y deben tener unidades compatibles.
• n es un número entero que especifica el orden polinomial. Debe ser inferior al número total de puntos de datos: 1 ≤ n ≤ length(Y) − 1. En caso contrario, el problema estará restringido, pero no tendrá una solución única.
• “terms” es una cadena que especifica los términos, o los factores e interacciones, que se deben incluir en la regresión polinomial. "A B AB AA BB" significa que el polinomio contiene los siguientes términos:
c0 + c1 ∙ A + c2 ∙ B + c3 ∙ A ∙ B + c4 ∙ A2 + c5 ∙ B2
Para los separadores, se puede usar un espacio, una coma, dos puntos o un punto y coma.
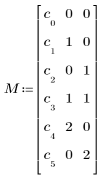
• M es una matriz que especifica un polinomio con valores de prueba para los coeficientes en la primera columna y la potencia de las variables independientes para cada término en las columnas restantes. Con respecto al polinomio descrito anteriormente, defina M como sigue:
• conf (opcional) es el límite de confianza deseado, un porcentaje que se expresa con un número comprendido entre 0 y 1, ambos inclusive. Por defecto, conf = 0.95 para un intervalo de confianza del 95 %.