Ejemplo: calidad de ajuste
Use las funciones polyfit y polyfitstat para llevar a cabo una regresión lineal y un análisis de varianza para probar la calidad del ajuste.
1. Defina una tabla de datos experimentales para un proceso de polímeros. La temperatura de reacción t y la velocidad de avance del catalizador fr afectan a la viscosidad vy del polímero.

Calidad de ajuste
2. Llame a la función polyfit para modelar los datos como una regresión lineal.
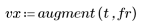
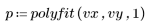
3. Calcule la viscosidad prevista para cada ajuste de temperatura y velocidad de avance.
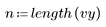
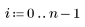
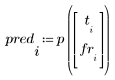
4. Calcule los residuales (la diferencia entre los valores calculados y los valores medidos del modelo).
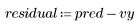
5. Trace los residuales con respecto a la viscosidad observada, la temperatura y la velocidad de avance.
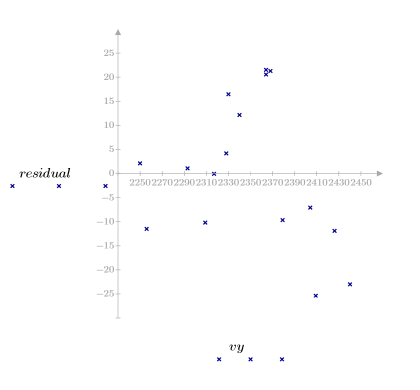
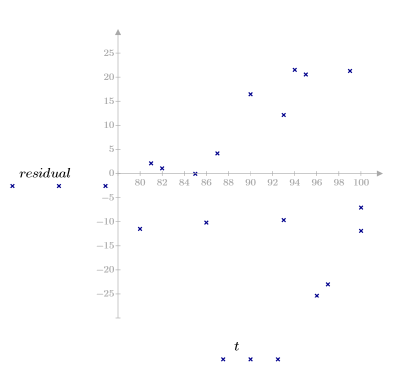
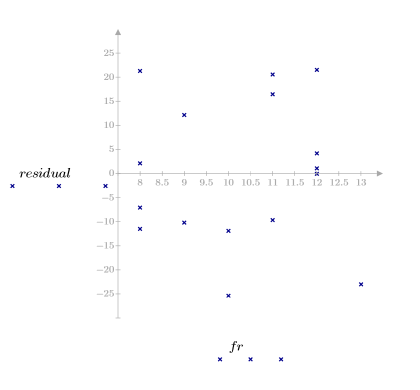
Los gráficos de residuales indican que las varianzas de la viscosidad observada y la temperatura aumentan a medida que la magnitud de la viscosidad y la temperatura, respectivamente, aumentan.
6. Llame a polyfitstat para calcular varias estadísticas para el modelo lineal. Visualice la matriz ANOVA que devuelve polyfitstat en la fila 8.
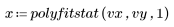
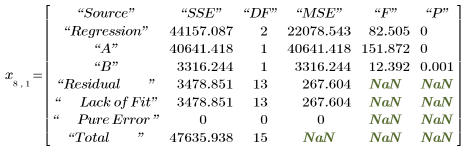
En la matriz de análisis de varianza (ANOVA), las fuentes de varianza se dividen entre componentes de regresión y residuales. El componente de regresión, a su vez, se divide entre los diferentes coeficientes de regresión. Sin embargo, no puede distinguir entre la falta de ajuste y el error puro del residual, ya que los resultados del experimento vy no tienen réplicas.
Cálculo y uso de la tabla de análisis de varianza (ANOVA) para la regresión
1. Calcule la suma de los cuadrados debido a error (SSE).
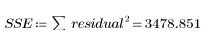
SSE es igual a χ2, una métrica general para la bondad de ajuste. Esta es la cantidad minimizada al calcular la solución de mínimos cuadrados. El error es una medida del ajuste del modelo a los datos. Muestra la cantidad de desviación que no está justificada por la regresión.
2. Defina los grados de libertad de movimiento para el error df_error con respecto al total de grados de libertad de movimiento df_total y los grados de libertad de movimiento para los parámetros df_param. Los grados de libertad de movimiento equivalen a la longitud de los datos menos el número de parámetros de ajuste.
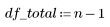
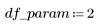
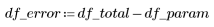
3. Defina la suma de cuadrados debida a la regresión (SSR) con respecto a la suma total de cuadrados (SST).
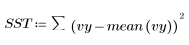
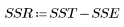
4. Defina el cuadrado medio del error (MSE) y el cuadrado medio de regresión (MSR). Divida el error por los grados de libertad de movimiento adecuados.
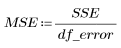
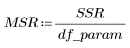
5. Forme un análisis de tabla de varianza para caracterizar el ajuste.
Suma de cuadrados | DF | Cuadrado medio | Factor F | |
|---|---|---|---|---|
Regresión | 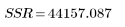 | 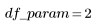 | 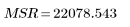 | 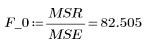 |
Error | 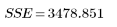 | 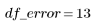 | 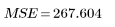 | |
Total | 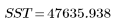 | 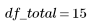 |
La tabla anterior se puede comparar con la matriz de análisis de varianza (ANOVA) polyfitstat.
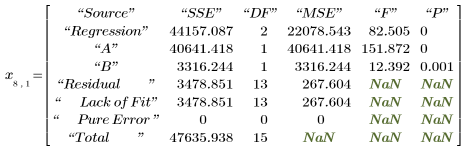
6. Realice un cálculo aproximado del ajuste del modelo a los datos:
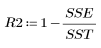
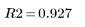
Esto indica que el 92.7 % de la variabilidad de la viscosidad está justificado por el modelo de regresión lineal.
7. Defina el nivel de significancia para una prueba de hipótesis que compruebe si el modelo se ajusta a los datos.
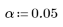
8. Calcule el valor F crítico.
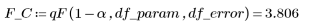
9. Compruebe la hipótesis de que el modelo se ajusta a los datos.
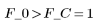
Acepte la hipótesis. La viscosidad del polímero se puede predecir con este modelo de regresión lineal.
Referencia
Montgomery, D.C., Design and Analysis of Experiments, 5th ed., John Wiley & Sons, New York, 2001, págs. 398