Ejemplo: Identificación de las observaciones influyentes
Use la función polyfitstat para comprobar las observaciones utilizadas para crear una regresión polinomial multivariada.
1. Defina una matriz que contenga las muestras tomadas de 20 personas sanas con edades entre 25 y 34 años.
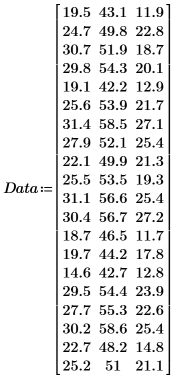
Las columnas de la matriz representan el grosor del pliegue cutáneo en los tríceps, la circunferencia del muslo y la grasa corporal, respectivamente, para cada una de las 20 personas.
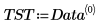
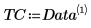
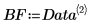
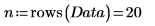
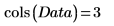
3. Use la función augment para definir la matriz BM como las dos primeras columnas de la matriz. Utilice estas mediciones para predecir la cantidad de grasa de las personas.
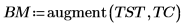
4. Llame a la función polyfitstat para modelar el experimento con una regresión de primer orden y calcular las estadísticas de regresión.
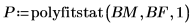
5. Muestre la matriz de coeficientes de regresión que se encuentra en la fila 7 de la salida P.
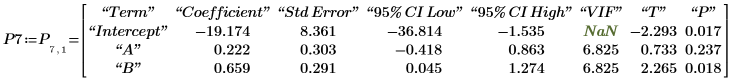
6. Calcule los coeficientes de regresión mediante el cálculo de matrices.
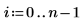
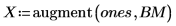
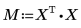
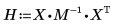
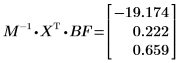
Los coeficientes de regresión se ajustan a la siguiente ecuación:
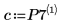
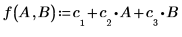
7. Utilice la ecuación de regresión para calcular la cantidad prevista de grasa corporal. Compare estos valores con la cantidad de grasa corporal medida.
 |  |
8. Utilice la función submatrix para mostrar las estadísticas del modelo encontradas en las primeras filas de la matriz de salida P.

La primera estadística es la desviación estándar con respecto a la regresión.
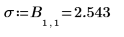
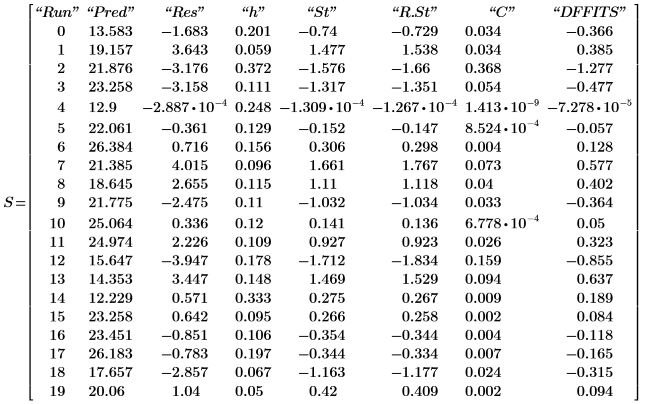
9. Muestre los diagnósticos del modelo que aparecen en la última matriz anidada de la matriz de salida P.
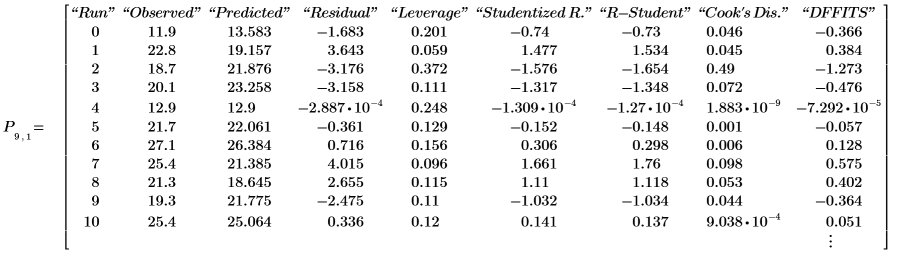
Los valores observados y previstos corresponden a los valores mostrados en el paso 7. Los residuales son la diferencia entre los valores observados y los previstos:
10. Calcule los residuales, o la diferencia entre los valores observados y los previstos.
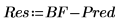
11. Use la función diag para calcular los valores de apalancamiento, o los valores diagonales, de la matriz H.
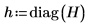
12. Calcule los residuales estudentizados.
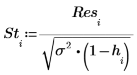
A continuación, se calculan los residuales estudentizados externamente, o R de Student. La constante p es el número de coeficientes calculados para la regresión y S2 es un cálculo aproximado de s2 basado en un conjunto de datos del que se ha quitado la observación i.
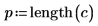
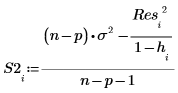
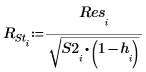
13. Utilice la distancia de Cook para medir la influencia general de un punto borrado en una regresión lineal.
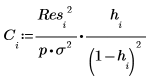
14. Calcule la diferencia entre los valores previstos al incluir todas las observaciones en el ajuste y los valores previstos al omitir la observación i.
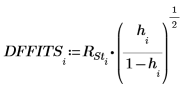
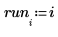
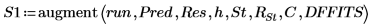
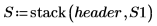
16. Use las funciones max y qt para determinar el valor R de Student más alto del conjunto de datos. Utilice la prueba de Bonferroni para decidir si la observación correspondiente es un valor atípico.
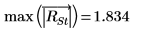
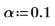
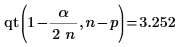
El valor R de Student mayor es menor que la prueba de Bonferroni, lo que indica que la observación correspondiente no es un valor atípico.
17. Determine el valor DFFITS máximo.
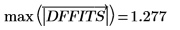
El valor es mayor que 1, pero se acerca a 1 lo suficiente como para que la observación correspondiente no tenga necesariamente un impacto.
18. Cree un gráfico de influencias de índice trazando las distancias de Cook con respecto a las ejecuciones.
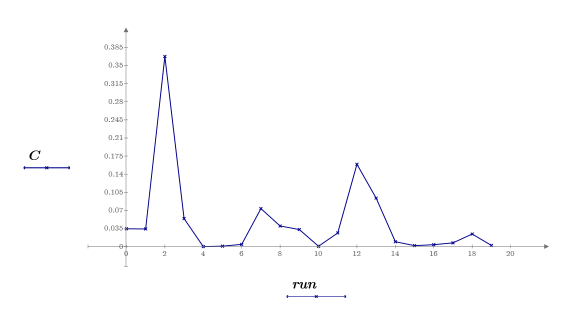
La observación para run2 es la más influyente del conjunto de datos. La observación para run12 identificada en el paso 10 también es influyente, pero mucho menos que para run2.
Referencia
Referencia: Neter, J., Kutner, M.H., Nachtsheim, C.J., Wasserman, W., Applied Linear Statistical Models, 4th ed., McGraw-Hill/Irwin, Boston, 1996, pág. 375