ODE Solvers
• Each of the functions below returns an (intvls+1)×(n+1) solution matrix, where n is the number of unknowns. The first column of the matrix contains the values of x at which the solutions are evaluated. These values are (intvls + 1) evenly spaced numbers between x1 and x2. The remaining columns contain the values of the solutions y0,y1,...,yn-1 corresponding to the values of x in the first column.
• For the solvers rkfixed, RkAdapt, Bulstoer, Stiffb, and Stiffr, you can specify a scalar tolerance for the solution by defining the variable TOL before calling the solver. For example, you can set the tolerance for all variables as 10-6:
TOL:=10-6
TOL does not affect the tolerances for the solvers Adams, BDF, or Radau. For these solvers, you must use the optional argument tol to specify tolerances.
• You may wish to use ODE solve blocks to simplify the entry of your equations and initial conditions.
Solvers for Nonstiff Systems
• Adams(init, x1, x2, intvls, D, [tol])—Uses Adams methods.
• rkfixed(init, x1, x2, intvls, D)—Uses the fourth order Runge-Kutta fixed-step method.
• Rkadapt(init, x1, x2, intvls, D)—Uses the fourth order Runge-Kutta with adaptive step-size.
• Bulstoer(init, x1, x2, intvls, D)—Uses the Bulirsch-Stoer method, which is slightly more accurate than Runge-Kutta, but requires a smoothly varying system.
Solvers for Stiff Systems
Use these functions to solve stiff or algebraic ODE problems.
• BDF(init, x1, x2, intvls, D, [J], [tol])—Uses backward differentiation formula methods. You can use either of the optional arguments J or tol and omit the other.
• Radau(init, x1, x2, intvls, D, [J], [M], [tol])—Uses the Radau5 method. You can use any combination of the optional arguments J, M, and tol and omit the options you do not wish to use.
• Stiffb(init, x1, x2, intvls, D, AJ)—Uses the Bulirsch-Stoer method.
• Stiffr(init, x1, x2, intvls, D, AJ)—Uses Rosenbrock method.
Hybrid Solver
• AdamsBDF(init, x1, x2, intvls, D, [J], [tol])—Determines whether a system is stiff or nonstiff and calls Adams or BDF accordingly. You can use either of the optional arguments J or tol and omit the other.
Arguments
• init is either a vector of n real initial values, where n is the number of unknowns, or a single scalar initial value, in the case of a single ODE.
• x1 and x2 are real, scalar endpoints of the interval over which the solution to the ODEs is evaluated. The initial values in init are the values of the ODE functions evaluated at x1
• intvls is the integer number of discretization intervals used to interpolate the solution function. The number of solution points is the number of intervals + 1.
• D is a vector function of the form D(x,y) specifying the right-hand side of the system.
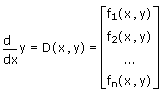
• tol (optional) is a real value, or a vector of real values, specifying tolerances for each independent variable in the system. The tolerance is the required accuracy for a solution variable.
◦ You should set tol to be less than or equal to 10-5. Depending on the scale of the problem and the relative step size used, you may need to reduce the value of TOL to get appropriate solutions. The smaller the value of tol, the more steps the solver algorithm performs to achieve the required accuracy.
◦ If you are solving a system of equations, setting tol to be a scalar specifies the same tolerance for all variables in the system. Setting tol to be a vector, whose length equals the numbers of variables in the system, specifies individual tolerances for each of the variables.
• J (optional) is a function of the form J(x, y) that returns the Jacobian matrix: the matrix of partial derivatives of the functions in D with respect to y0, y1, ... yn−1.
• M (optional) is a real matrix representing any coupling between the variables in the form M · dy/dt = f(t, y).
• AJ is a function of the form AJ(x, y) that returns the augmented Jacobian, whose first column contains the partial derivatives, with respect to x, of the functions on the right-hand side of the system. The remaining columns are the columns of the Jacobian J, containing the partial derivatives with respect to y0,y1, ... yn−1.
The D, J, and AJ functions are provided to the solver without their arguments, and the functions yn(x) are specified in D, J, and AJ without their argument.
The second argument to D, J, and AJ must be subscripted as a vector, even if there is only a single entry.
Additional Information
• Functions Radau and Rkadapt use nonuniform step sizes internally when they solve the differential equation, adding more steps in regions of greater variation of the solution, but return the solution at the number of equally spaced points specified in intvls.
• An advantage to using Radau is that no Jacobian input is needed, although if J is readily available, using it tends to increase accuracy.